
����Ŀ��Ϊ�˵���ij��ѧѧ��������������ʱ�䣬�����![]() ��������
��������![]() ��Ů�������˲��������ʾ����飬�õ������µ�ͳ�ƽ����
��Ů�������˲��������ʾ����飬�õ������µ�ͳ�ƽ����
��1����������ʱ����Ƶ���ֲ�����
����ʱ�䣨���ӣ� |
|
|
|
|
|
���� | 5 | 25 | 30 | 25 | 15 |
��2��Ů������ʱ����Ƶ���ֲ�����
����ʱ�䣨���ӣ� |
|
|
|
|
|
���� | 10 | 20 | 40 | 20 | 10 |
��1�����ô�ѧ����Ů��![]() �ˣ��Թ�����������ʱ�䲻����
�ˣ��Թ�����������ʱ�䲻����![]() ���ӵ�������
���ӵ�������
��2����ɱ�3��![]() �����������ش��ܷ���
�����������ش��ܷ���![]() �İ�����Ϊ��ѧ����������ʱ�����Ա��й�����
�İ�����Ϊ��ѧ����������ʱ�����Ա��й�����
��3���ӱ�3��������������ʱ������![]() ��������������ʱ�䲻����
��������������ʱ�䲻����![]() ���������������÷ֲ�����ķ�����ȡһ������Ϊ
���������������÷ֲ�����ķ�����ȡһ������Ϊ![]() ���������ٴ�����ȡ���ˣ���������һ������ʱ�䳬��
���������ٴ�����ȡ���ˣ���������һ������ʱ�䳬��![]() ���ӵĸ���.��3��
���ӵĸ���.��3��
����ʱ������60���� | ����ʱ�䲻����60���� | �ϼ� | |
���� | |||
�� | |||
�ϼ� |
���� ������
������![]() ��
��
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���𰸡���1��![]() ����2������������3��
����2������������3��![]()
��������
��1��ֱ�Ӹ��ݱ�����ϵ����õ���.
��2������������������![]() ���õ���.
���õ���.
��3��![]() ��������ʱ������
��������ʱ������![]() ���ӵ���
���ӵ���![]() �ˣ���Ϊ
�ˣ���Ϊ![]() ������ʱ�䲻����
������ʱ�䲻����![]() ���ӵ���
���ӵ���![]() �ˣ���Ϊ
�ˣ���Ϊ![]() ���г����������ͳ������������������õ�����.
���г����������ͳ������������������õ�����.
��1�����������ʱ�䲻����![]() ���ӵ�����
���ӵ�����![]() ������������
������������![]() ����ã�
����ã�![]() .
.
���Թ�����������ʱ�䲻����![]() ���ӵ�������
���ӵ�������![]() ��.
��.
��2��������Ŀ�������ݵõ�������������
����ʱ�䲻����60���� | ����ʱ�䲻����60���� | �ϼ� | |
���� | 60 | 40 | 100 |
�� | 70 | 30 | 100 |
130 | 70 | 200 |
����![]() ��
��
��ˣ�û��![]() �İ�����Ϊ��ѧ����������ʱ�����Ա��йء�.
�İ�����Ϊ��ѧ����������ʱ�����Ա��йء�.
��3����Ϊ����ʱ������![]() ����������ʱ�䲻����
����������ʱ�䲻����![]() ���ӵ�����֮��Ϊ
���ӵ�����֮��Ϊ![]() ��
��
����![]() ��������ʱ������
��������ʱ������![]() ���ӵ���
���ӵ���![]() �ˣ���Ϊ
�ˣ���Ϊ![]() ��
��
����ʱ�䲻����![]() ���ӵ���
���ӵ���![]() �ˣ���Ϊ
�ˣ���Ϊ![]() ��������ȡ���˵����л����¼�Ϊ��
��������ȡ���˵����л����¼�Ϊ��![]() ����
����![]() �֣�
�֣�
���С�������һ������ʱ�䳬��![]() ���ӡ�������
���ӡ�������![]() �֣���
�֣���![]() .
.


 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼһ����ֱ������![]() �У�
�У�![]() �ֱ�Ϊ
�ֱ�Ϊ![]() �����ȷֵ㣬
�����ȷֵ㣬![]() ,
, ![]() ��
��![]() ��
��![]() ��������
��������![]() �۵�ʹ�õ�
�۵�ʹ�õ�![]() ��
��![]() �غϣ���ͼ����ʾ������
�غϣ���ͼ����ʾ������![]() .
.
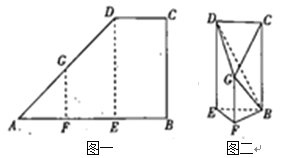
��1����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2�����![]() ��ƽ��
��ƽ��![]() �ľ���.
�ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�н�����һ���Լ![]() �Ľӽ������εĻĵأ��ط��������ڴ˽�һ���ۺ������й㳡������Ҫ������ͼ��ʾ��һ�����γ��أ����������Ϊ3000ƽ���ף�������Ӱ����Ϊͨ����ͨ������Ϊ2�ף��м�������������������ܽ�������Ϊ�˶����أ���������С������״��ͬ�����ܽ��˶�����ռ�����Ϊ
�Ľӽ������εĻĵأ��ط��������ڴ˽�һ���ۺ������й㳡������Ҫ������ͼ��ʾ��һ�����γ��أ����������Ϊ3000ƽ���ף�������Ӱ����Ϊͨ����ͨ������Ϊ2�ף��м�������������������ܽ�������Ϊ�˶����أ���������С������״��ͬ�����ܽ��˶�����ռ�����Ϊ![]() ƽ���ף�
ƽ���ף�
��1���ֱ���![]() ��ʾ
��ʾ![]() ��
��![]() �ĺ�����ϵʽ��������������
�ĺ�����ϵʽ��������������
��2�����������ʹ![]() ȡ�����ֵ����������ֵ��
ȡ�����ֵ����������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��b��R������x�ķ��̣�x2��ax+1����x2��bx+1����0���ĸ�ʵ��������qΪ���ȵĵȱ����У���q��[![]() ��2]����ab��ȡֵ��ΧΪ______��
��2]����ab��ȡֵ��ΧΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ����֪
����֪![]() .
.
��1����![]() ��������
��������![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2��������![]() ���㣺
���㣺![]() .
.
��������![]() ��ͨ�ʽ��
��ͨ�ʽ��
���Ƿ����������![]() ��ʹ��
��ʹ��![]() �����������ڣ��������
�����������ڣ��������![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
��![]() ��������Ϊ
��������Ϊ![]() ��ֱ��
��ֱ��![]() ��
��![]() ����ԭ��ΪԲ�ģ�����Բ
����ԭ��ΪԲ�ģ�����Բ![]() �Ķ̰��᳤Ϊ�뾶��Բ����.
�Ķ̰��᳤Ϊ�뾶��Բ����.![]() Ϊ�㣬����
Ϊ�㣬����![]() ��ֱ�߽���Բ
��ֱ�߽���Բ![]() ��
��![]() ��
��![]() ���㣬ֱ��
���㣬ֱ��![]() ��
��![]() �ֱ�ֱ��
�ֱ�ֱ��![]() ��
��![]() ��
��![]() ����.
����.
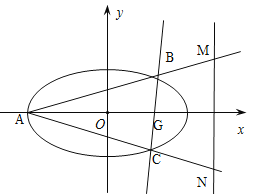
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2�����߶�![]() Ϊֱ����Բ�Ƿ�����㣿���ǣ�д�����ж�������ꣻ�����ǣ���˵������.
Ϊֱ����Բ�Ƿ�����㣿���ǣ�д�����ж�������ꣻ�����ǣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�����ABCD�����Σ���ADC��60�㣬����PDC���������Σ�ƽ��PDC��ƽ��ABCD��CD��2��MΪPB���е�.

(1)��֤��PA��ƽ��CDM��
(2)������D��MC��B������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ı���ABCDΪ���Σ�GΪAC��BD���㣬![]() ��
��
��I��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��II����![]() ��
��![]() ����
����![]() �����Ϊ
�����Ϊ![]() ����������IJ����.
����������IJ����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ʱ��֤��������
ʱ��֤��������![]() ��������㣻
��������㣻
��2����![]() ʱ������
ʱ������![]() ������
������![]() �ϵ���Сֵ.
�ϵ���Сֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com