
【题目】已知函数f(x)与g(x)分别是定义在R上的偶函数和奇函数,且f(x)﹣g(x)=x3﹣2﹣x , 则f(2)+g(2)=( )
A.4
B.﹣4
C.2
D.﹣2
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】知 ![]() =(2λsinx,sinx+cosx),
=(2λsinx,sinx+cosx), ![]() =(
=( ![]() cosx,λ(sinx﹣cosx))(λ>0),函数f(x)=
cosx,λ(sinx﹣cosx))(λ>0),函数f(x)= ![]()
![]() 的最大值为2.
的最大值为2.
(1)求函数f(x)的单调递减区间;
(2)在△ABC中,内角A,B,C的对边分别为a,b,c,cosA= ![]() ,若f(A)﹣m>0恒成立,求实数m的取值范围.
,若f(A)﹣m>0恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,E、F分别为棱BB1、BC的中点,则异面直线AB1与EF所成角的大小为( )
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣ax﹣lnx,a∈R.
(Ⅰ)若函数f(x)的图象在x=1处的切线斜率为1,求实数a的值;
(Ⅱ)当a≥﹣1时,记f(x)的极小值为H,求H的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,旅客从某旅游区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50米/分钟,在甲出发2分钟后,乙从A乘缆车到B,再从B匀速步行到C.假设缆车匀速直线运动的速度为130米/分钟,山路AC长1260米,经测量,cosA= ![]() ,cosC=
,cosC= ![]() .
. 
(1)求索道AB的长;
(2)问乙出发后多少分钟后,乙在缆车上与甲的距离最短?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱锥P﹣ABC的底面是等腰直角三角形,且∠ACB= ![]() ,侧面PAB⊥底面ABC,AB=PA=PB=2.则这个三棱锥的三视图中标注的尺寸x,y,z分别是( )
,侧面PAB⊥底面ABC,AB=PA=PB=2.则这个三棱锥的三视图中标注的尺寸x,y,z分别是( ) 
A.![]() ,1,
,1, ![]()
B.![]() ,1,1
,1,1
C.2,1, ![]()
D.2,1,1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩形ADEF和菱形ABCD所在平面互相垂直,如图,其中AF=1,AD=2,∠ADC= ![]() ,点N时线段AD的中点.
,点N时线段AD的中点. 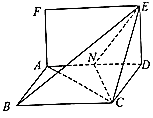
(Ⅰ)试问在线段BE上是否存在点M,使得直线AF∥平面MNC?若存在,请证明AF∥平面MNC,并求出 ![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(Ⅱ)求二面角N﹣CE﹣D的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=sin(ωx+φ)+cos(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期为π,且f(﹣x)=f(x),则( )
)的最小正周期为π,且f(﹣x)=f(x),则( )
A.f(x)在(0, ![]() )单调递增
)单调递增
B.f(x)在( ![]() ,
, ![]() )单调递减
)单调递减
C.f(x)在( ![]() ,
, ![]() )单调递增
)单调递增
D.f(x)在( ![]() ,π)单调递增
,π)单调递增
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com