
【题目】函数f(x)=x3+bx2+cx+d图象如图,则函数 ![]() 的单调递减区间为( )
的单调递减区间为( ) 
A.(﹣∞,﹣2)
B.[3,+∞)
C.[﹣2,3]
D.[ ![]() )
)
【答案】A
【解析】解:∵f(x)=x3+bx2+cx+d∴f'(x)=3x2+2bx+c
由函数f(x)的图象知,f'(﹣2)=0,f'(3)=0
∴b=﹣ ![]() ,c=﹣18
,c=﹣18
∴ ![]() =log2(x2﹣x﹣6)的定义域为:(﹣∞,﹣2)∪(3,+∞)
=log2(x2﹣x﹣6)的定义域为:(﹣∞,﹣2)∪(3,+∞)
令z=x2﹣5x﹣6,在(﹣∞,﹣2)上递减,在(3,+∞)上递增,且y=log2z
根据复合函数的单调性知,
函数 ![]() 的单调递减区间是(﹣∞,﹣2)
的单调递减区间是(﹣∞,﹣2)
故选A.
【考点精析】解答此题的关键在于理解复合函数单调性的判断方法的相关知识,掌握复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”,以及对对数函数的单调区间的理解,了解a变化对图象的影响:在第一象限内,a越大图象越靠低;在第四象限内,a越大图象越靠高.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案科目:高中数学 来源: 题型:
【题目】高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
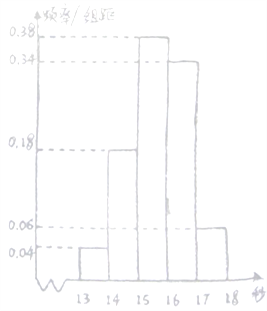
(1)请根据频率分布直方图估计该组数据的众数和中位数(精确到0.1);
(2)从成绩介于![]() 和
和![]() 两组的人中任取2人,求两人分布来自不同组的概率.
两组的人中任取2人,求两人分布来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABCA1B1C1中,D是BC的中点.

(1)求证:A1B∥平面ADC1;
(2)若AB⊥AC,AB=AC=1,AA1=2,求几何体ABD-A1B1C1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,设圆x2+y2-4x=0的圆心为Q.
(1)求过点P(0,-4)且与圆Q相切的直线的方程;
(2)若过点p(0,-4)且斜率为k的直线与圆Q相交于不同的两点A,B,以OA、OB为邻边做平行四边形OABC,问是否存在常数k,使得平行四边形OABC为矩形?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若方程![]() 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题:
①若C为椭圆,则![]() ;
;
②若C为双曲线,则![]() 或
或![]() ;
;
③曲线C不可能是圆;
④若![]() ,曲线C为椭圆,且焦点坐标为
,曲线C为椭圆,且焦点坐标为![]() ;
;
⑤若![]() ,曲线C为双曲线,且虚半轴长为
,曲线C为双曲线,且虚半轴长为![]() .
.
其中真命题的序号为____________.(把所有正确命题的序号都填在横线上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com