
分析 (1)点(2Sn+an,Sn+1)在f(x)=$\frac{1}{2}$x+$\frac{1}{3}$的图象上.可得Sn+1=$\frac{1}{2}(2{S}_{n}+{a}_{n})$+$\frac{1}{3}$,化为an+1=$\frac{1}{2}{a}_{n}$+$\frac{1}{3}$,变形为an+1-$\frac{2}{3}$=$\frac{1}{2}({a}_{n}-\frac{2}{3})$,利用等比数列的通项公式即可得出.
(2)cn=(an-$\frac{2}{3}$)n=$n×\frac{1}{{2}^{n}}$.利用“错位相减法”与等比数列的求和公式即可得出.
解答 解:(1)点(2Sn+an,Sn+1)在f(x)=$\frac{1}{2}$x+$\frac{1}{3}$的图象上.
∴Sn+1=$\frac{1}{2}(2{S}_{n}+{a}_{n})$+$\frac{1}{3}$,
化为an+1=$\frac{1}{2}{a}_{n}$+$\frac{1}{3}$,变形为an+1-$\frac{2}{3}$=$\frac{1}{2}({a}_{n}-\frac{2}{3})$,
∴数列$\{{a}_{n}-\frac{2}{3}\}$是等比数列,首项为$\frac{1}{2}$,公比为$\frac{1}{2}$.
∴an=$\frac{1}{2}×(\frac{1}{2})^{n-1}$+$\frac{2}{3}$=$(\frac{1}{2})^{n}$+$\frac{2}{3}$.
(2)cn=(an-$\frac{2}{3}$)n=$n×\frac{1}{{2}^{n}}$,
∴数列{cn}的前n项和Tn=$1×\frac{1}{2}$+2×$\frac{1}{{2}^{2}}$+$3×\frac{1}{{2}^{3}}$+…+$n×\frac{1}{{2}^{n}}$,
$\frac{1}{2}{T}_{n}$=$\frac{1}{{2}^{2}}$+$2×\frac{1}{{2}^{3}}$+…+$(n-1)×\frac{1}{{2}^{n}}$+n×$\frac{1}{{2}^{n+1}}$,
∴$\frac{1}{2}$Tn=$\frac{1}{2}+\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$-n×$\frac{1}{{2}^{n+1}}$=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-$n×\frac{1}{{2}^{n+1}}$=1-(2+n)×$\frac{1}{{2}^{n+1}}$,
∴Tn=2-$\frac{2+n}{{2}^{n}}$.
点评 本小题主要考查“错位相减法”、等比数列与等差数列的通项公式与前n项和公式等基础知识,考查运算求解能力,属于中档题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:解答题
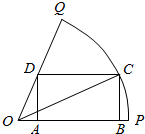 如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的运动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.
如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的运动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∪B=B | B. | A∩B=A | C. | A∪(CUB)=U | D. | (CUA)∪B=U |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=1,b=3 | B. | a=3,b=1 | C. | a=$\frac{1}{2}$,b=$\frac{3}{2}$ | D. | a=$\frac{3}{2}$,b=$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com