
(1)已知f(![]() +1)=x+2
+1)=x+2![]() ,求f(x),f(x+1),f(x2);?
,求f(x),f(x+1),f(x2);?
(2)已知二次函数f(x)满足f(0)=1,f(x+1)-f(x)=2x,求f(x);?
(3)已知f(x)+![]() )=2x+1,求f(x).?
)=2x+1,求f(x).?
解:(1)令u=![]() +1(x≥0),则
+1(x≥0),则![]() =u-1,即x=(u-1)2(u≥1),
=u-1,即x=(u-1)2(u≥1),
∴f(u)=(u-1)2+2(u-1)=u2-1(u≥1),即f(x)=x2-1(x≥1).?
∴f(x+1)=(x+1)2-1=x2+2x(x≥0),?
f(x2)=x4-1(x≤-1或x≥1).?
(2)设f(x)=ax2+bx+c,则f(0)=c=1,?
∴f(x+1)=a(x+1)2+b(x+1)+1=(ax2+bx+1)+(2ax+a+b).?
∴f(x+1)-f(x)=2ax+a+b=2x.?
∴![]() 即
即![]()
∴f(x)=x2-x+1.?
(3)∵f(x)+![]() )=2x+1, ①
)=2x+1, ①
∴以![]() 代上式中的x得f(
代上式中的x得f(![]() )+
)+![]() +1. ②
+1. ②
∴①-②×2得-![]() -2,即f(x)=
-2,即f(x)=![]() .?
.?
点评: 本例中(1)题是换元法,注意换元后变量的取值范围;(2)题是待定系数法,对于已知函数特征,如正、反比例函数,一、二次函数等可用此法;(3)题是通过变量替换消去f(![]() ),从而求出f(x)的解析式.
),从而求出f(x)的解析式.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
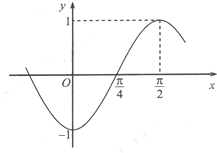 已知函数f(x)=Asin(ωx+φ),(ω>0,|ω|<π)部分图象如图所示.
已知函数f(x)=Asin(ωx+φ),(ω>0,|ω|<π)部分图象如图所示.| π |
| 4 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省高一10月阶段性检测数学试卷(解析版) 题型:解答题
(本题满分16分)某公司将进货单价为8元一个的商品按10元一个销售,每天可卖出100个,若这种商品的销售价每个上涨1元,则销售量就减少10个.
(1)求函数解析式;
(1)求销售价为13元时每天的销售利润;
(2)如果销售利润为360元,那么销售价上涨了几元?
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com