考点:与二面角有关的立体几何综合题,点、线、面间的距离计算
专题:综合题,空间位置关系与距离,空间角
分析:(1)连接AO,在△AOA1中,作OE⊥AA1于点E,则E为所求.可以证出OE⊥BB1,BC⊥OE而得以证明.在Rt△A1OA中,利用直角三角形射影定理得出AE.
(2)分别以OA,OB,OA1所在直线为x,y,z轴,建立空间直角坐标系,求出平面A1B1C的法向量,利用向量的夹角公式求平面A1B1C与平面BB1C1C夹角的余弦值,从而可得正弦值.
解答:
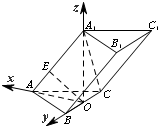
(1)证明:连接AO,在△AOA
1中,作OE⊥AA
1于点E,
∵AA
1∥BB
1,∴OE⊥BB
1,
∵A
1O⊥平面ABC,∴BC⊥平面AA
1O,∴BC⊥OE,
∴OE⊥平面BB
1C
1C,
又AO=
=1,AA
1=
得AE=
=.…4′
(2)解:建立如图所示空间直角坐标系,则A(1,0,0),B(0,2,0),C(0,-2,0),A
1(0,0,2)
由
=,得点E得坐标是
(,0,).
设平面A
1B
1C的法向量是
=(x,y,z),
由
得
令y=1,得x=2,z=-1,
=(2,1,-1)∴
cos?,>==∴平面A
1B
1C与平面BB
1C
1C夹角的正弦值为
.…12′.
点评:本题考查空间直线和平面位置关系的确定,要熟练掌握应用空间有关的性质、定理;还考查了二面角大小求解,建立空间直角坐标系利用向量法是关键.

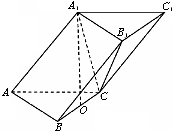 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1= (1)证明:连接AO,在△AOA1中,作OE⊥AA1于点E,
(1)证明:连接AO,在△AOA1中,作OE⊥AA1于点E,

 阅读快车系列答案
阅读快车系列答案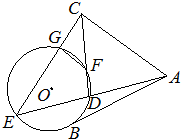 如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB,CE交⊙O于点G.
如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB,CE交⊙O于点G.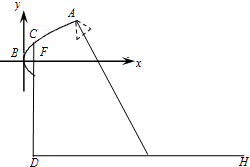 为了迎接青奥会,南京将在主干道统一安装某种新型节能路灯,该路灯由灯柱和支架组成.在如图所示的直角坐标系中,支架ACB是抛物线y2=2x的一部分,灯柱CD经过该抛物线的焦点F且与路面垂直,其中C在抛物线上,B为抛物线的顶点,DH表示道路路面,BF∥DH,A为锥形灯罩的顶,灯罩轴线与抛物线在A处的切线垂直.安装时要求锥形灯罩的顶到灯柱的距离是1.5米,灯罩的轴线正好通过道路路面的中线.
为了迎接青奥会,南京将在主干道统一安装某种新型节能路灯,该路灯由灯柱和支架组成.在如图所示的直角坐标系中,支架ACB是抛物线y2=2x的一部分,灯柱CD经过该抛物线的焦点F且与路面垂直,其中C在抛物线上,B为抛物线的顶点,DH表示道路路面,BF∥DH,A为锥形灯罩的顶,灯罩轴线与抛物线在A处的切线垂直.安装时要求锥形灯罩的顶到灯柱的距离是1.5米,灯罩的轴线正好通过道路路面的中线.