
分析 (Ⅰ)利用x=10时,y=9.2,代入y=$\frac{51}{50}$x-ax2-ln$\frac{x}{10}$,求出a,得到函数的解析式.
(Ⅱ)对f(x)求导,得f′(x),通过f′(x)=0求出极值点,判断函数的导数符号,得到函数的单调性,然后推出最值点即可.
解答 (本小题满分12分)
解:(Ⅰ)因当x=10时,y=9.2,代入y=$\frac{51}{50}$x-ax2-ln$\frac{x}{10}$,
即$\frac{51}{50}×10-a×{10}^{2}-ln1=9.2$,解得a=$\frac{1}{100}$.
所以y=$\frac{51}{50}$x-$\frac{1}{100}$x2-ln$\frac{x}{10}$,x∈(1,t]….(4分)
(Ⅱ)对f(x)求导,得f(x)=$\frac{51}{50}-\frac{x}{50}-\frac{1}{x}$=-$\frac{{x}^{2}-51x+50}{50x}$=$-\frac{(x-1)(x-50)}{50x}$,
令f′(x)=0得x=1(不合题意),或x=50
当1<x<50时,f′(x)>0,即f(x)递增,当x>50时,f′(x)<0,即f(x)递减.
①当t>50时,
x∈(1,50)时,f′(x)>0,即f(x)在(1,50)递增,
x∈(50,t)f′(x)<0,即f(x)在(50,t)递减…(8分)
故当x=50时,y取得最大值.
②当t<=50时,
x∈(1,t)时,f′(x)>0,即f(x)在(1,t)递增,
当x=t时,y取得最大值.…(12分)
点评 本题考查函数的导数的应用,函数的单调性以及好的最值的求法,正确求出函数的解析式是基础,利用导数求解是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | a<c<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①与② | B. | ①与④ | C. | ②与③ | D. | ②与④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
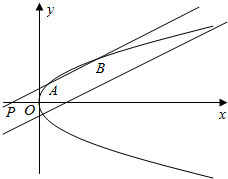 如图,已知抛物线C:y2=4x,点P(a,0),其中a<0,过点P作直线l1:x=my+a,与C交于不同的两点A,B
如图,已知抛物线C:y2=4x,点P(a,0),其中a<0,过点P作直线l1:x=my+a,与C交于不同的两点A,B查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com