
(本题满分12分)某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学 成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理 成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
| | 数学成绩优秀 | 数学成绩不优秀 | 合 计 |
| 物理成绩优秀 | | | |
| 物理成绩不优秀 | | | |
| 合 计 | | | 20 |
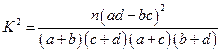 ,其中
,其中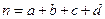 为样本容量;
为样本容量;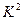 的临界值参考表:
的临界值参考表: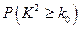 | 0.010 | 0.005 | 0.001 |
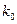 | 6.635 | 7.879 | 10.828 |
数学成绩优秀 数学成绩不优秀 合 计 物理成绩优秀 5 2 7 物理成绩不优秀 1 12 13 合 计 6 14 20
学生的数学成绩与物理成绩之间有关系
故从20名学生中抽出1名,抽到的学生数学成绩与物理成绩至少有一门不优秀的概率为
解析解:(1)2×2列联表为(单位:人): 数学成绩优秀 数学成绩不优秀 合 计 物理成绩优秀 5 2 7 物理成绩不优秀 1 12 13 合 计 6 14 20
…4分
(2)提出假设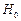 :学生数学成绩与物理成绩之间没有关系.
:学生数学成绩与物理成绩之间没有关系.
根据列联表可以求得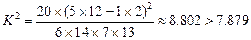 . …6分
. …6分
当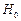 成立时,
成立时,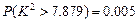 .所以我们有
.所以我们有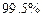 的把握认为:学生的数学成绩与物理成绩之间有关系. …8分
的把握认为:学生的数学成绩与物理成绩之间有关系. …8分
(3)由(1)可知数学成绩与物理成绩都优秀的学生的人数为5人,则数学成绩与物理成绩至少有一门不优秀的学生人数为15人. …10分
故从20名学生中抽出1名,抽到的学生数学成绩与物理成绩至少有一门不优秀的概率为 . …12分
. …12分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
(12分)为考察性别与是否喜欢饮酒之间的关系,在某地区随机抽取290人,得到如下表:
| | 喜欢饮酒 | 不喜欢饮酒 |
| 男 | 101 | 45 |
| 女 | 124 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某农场种植火龙果的成本x(单位:万元)与收益y(单位:万元)之间关系如下:
| x | 2 | 4 | 6 | 8 | 10 |
| Y | 10 | 13 | 15 | 18 | 20 |

 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校为了调查喜欢语文学科与性别是否有关系,随机调查了50名学生,男生中有12人不喜欢语文,有10人喜欢语文,女生中有8人不喜欢语文,有20人喜欢语文,根据所给数据,
(1)写出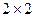 列联表;
列联表;
(2)由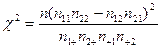 ,及临界值3.841和6.635作统计分析推断。
,及临界值3.841和6.635作统计分析推断。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂有工人1000名, 其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)。
(I)求甲、乙两工人都被抽到的概率,其中甲为A类工人,乙为B类工人;
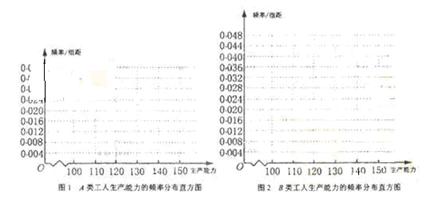
(II)从A类工人中的抽查结果和从B类工人中的抽插结果分别如下表1和表2.
表1:
| 生产能力分组 | 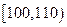 | 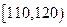 | 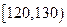 | 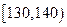 | 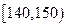 |
| 人数 | 4 | 8 | 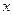 | 5 | 3 |
| 生产能力分组 | 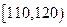 | 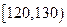 | 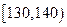 | 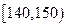 |
| 人数 | 6 | y | 36 | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
3位数学家,4位物理学家,站成两排照像.其中前排3人后排4人,要求数学家要相邻,则不同的排队方法共有( )
| A.5040种 | B.840种 | C.720种 | D.432种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
为了研究某高校大学新生学生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图,如图.已知前4组的频数从左到右依次是等比数列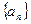 的前四项,后6组的频数从左到右依次是等差数列
的前四项,后6组的频数从左到右依次是等差数列 的前六项.
的前六项.
(I)求等比数列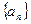 的通项公式;
的通项公式;
(II)求等差数列 的通项公式;
的通项公式;
(III) 若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率
若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老人,结果如下:
(Ⅰ)估计该地区老年人中,需要志愿提供帮助的老年人的比例;
(Ⅱ)能否有99℅的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(Ⅲ)根据(Ⅱ)的结论,能否提出更好的调查办法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由。
附: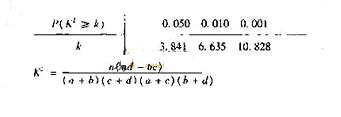
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com