
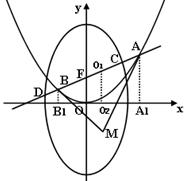
如图所示:已知过抛物线 的焦点F的直线
的焦点F的直线 与抛物线相交于A,B两点。
与抛物线相交于A,B两点。
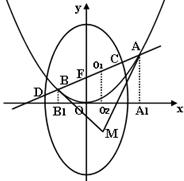
(1)求证:以AF为直径的圆与x轴相切;
(2)设抛物线 在A,B两点处的切线的交点为M,若点M的横坐标为2,求△ABM的外接圆方程;
在A,B两点处的切线的交点为M,若点M的横坐标为2,求△ABM的外接圆方程;
(3)设过抛物线 焦点F的直线
焦点F的直线 与椭圆
与椭圆 的交点为C、D,是否存在直线
的交点为C、D,是否存在直线 使得
使得 ,若存在,求出直线
,若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
(1)根据题意只要证明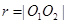 ∴以线段AF为直径的圆与x轴相切
∴以线段AF为直径的圆与x轴相切
(2)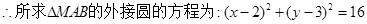
(3)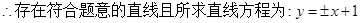 。
。
【解析】
试题分析:(1)解法一(几何法)设线段AF中点为 ,过
,过 作
作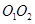 垂直于x轴,垂足为
垂直于x轴,垂足为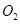 ,则
,则
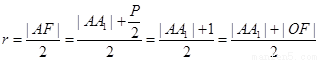 , 2分
, 2分
又∵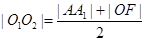 ,
3分
,
3分
∴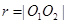 ∴以线段AF为直径的圆与x轴相切。
4分
∴以线段AF为直径的圆与x轴相切。
4分
解法二(代数法)设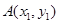 ,线段AF中点为
,线段AF中点为 ,过
,过 作
作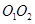 垂直于x轴,
垂直于x轴,
垂足为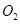 ,则
,则 ,
,
∴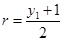 .
2分
.
2分
又∵点 为线段AF的中点,∴
为线段AF的中点,∴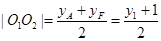 ,
3分
,
3分
∴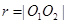 ,
,
∴以线段AF为直径的圆与x轴相切。 4分
(2)设直线AB的方程为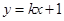 ,
,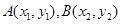 ,
,
由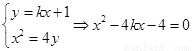 ,
,
∴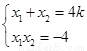 .
5分
.
5分
由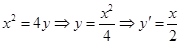 ,
,
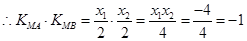 ,
, 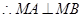 6分
6分
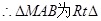 ,故
,故 的外接圆圆心为线段
的外接圆圆心为线段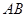 的中点。
的中点。
设线段AB中点为点P,易证⊙P与抛物线的准线相切,切点为点M ,
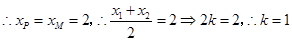 . 7分
. 7分
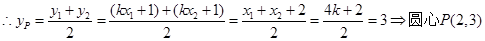 8分
8分
又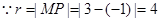 ,
,
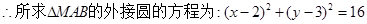 . 9分
. 9分
(3)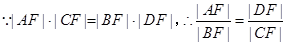 ,设
,设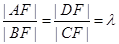 ,10分
,10分
则 ,设
,设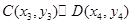 ,则
,则
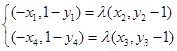
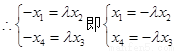 11分
11分
将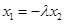 代入
代入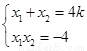 可得:
可得: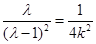 . ① 12分
. ① 12分
由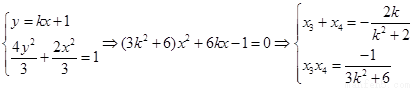 ,
,
联立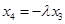 可得
可得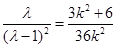 ,②
13分
,②
13分
联立①②可得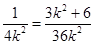 ,解得
,解得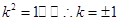 .
.
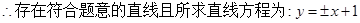 。
14分
。
14分
考点:直线与椭圆的位置关系
点评:主要是考查了直线与椭圆的位置关系的运用,属于中档题。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
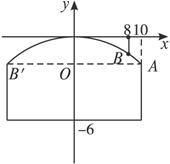
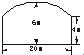 某大桥在涨水时有最大跨度的中央桥孔如图所示,已知上部呈抛物线形,跨度为20 m,拱顶距水面6 m,桥墩高出水面4 m,现有一货船欲过此孔,该货船水下宽度不超过18 m,目前吃水线上部分中央船体高5 m,宽16 m,且该货船在现在状况下还可多装1000 t货物,但每多装150 t货物,船体吃水线就要上升0.04 m,若不考虑水下深度,该货船在现在状况下能否直接或设法通过该桥孔?为什么?
某大桥在涨水时有最大跨度的中央桥孔如图所示,已知上部呈抛物线形,跨度为20 m,拱顶距水面6 m,桥墩高出水面4 m,现有一货船欲过此孔,该货船水下宽度不超过18 m,目前吃水线上部分中央船体高5 m,宽16 m,且该货船在现在状况下还可多装1000 t货物,但每多装150 t货物,船体吃水线就要上升0.04 m,若不考虑水下深度,该货船在现在状况下能否直接或设法通过该桥孔?为什么?查看答案和解析>>
科目:高中数学 来源:101网校同步练习 高二数学 苏教版(新课标·2004年初审) 苏教版 题型:044
某大桥在涨水时有最大跨度的中央桥孔如图所示,已知上部呈抛物线形,跨度为20 m,拱顶距水面6 m,桥墩高出水面4 m,现有一货船欲过此孔,该货船水下宽度不超过18 m,目前吃水线上部分中央船体高5 m,宽16 m,且该货船在现在状况下还可多装1000 t货物,但每多装150 t货物,船体吃水线就要上升0.04 m,若不考虑水下深度,该货船在现在状况下能否直接或设法通过该桥孔?为什么?

查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2006年高考第一轮复习数学:8.6 圆锥曲线的应用(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com