
(本题满分8分)
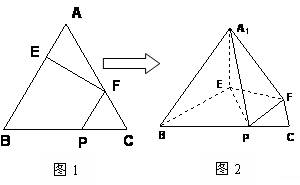 在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△AEF沿EF折起到
在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△AEF沿EF折起到![]() 的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求二面角A1-BP-E的大小。
(本题满分8分)
解:不妨设正三角形的边长为3,则
(I)在图1中,取BE的中点D,连结DF,
∵AE∶EB=CF∶FA=1∶2,∴AF=AD=2,而∠A=60o,∴△ADF为正三角形。
又AE=DE=1,∴EF⊥AD。
在图2中,A1E⊥EF,BE⊥EF,∴∠A1EB为二面角A1-EF-B的一个平面角,
由题设条件知此二面角为直二面角,∴A1E⊥BE。
又BE![]() EF=E,∴A1E⊥面BEF,即A1E⊥面BEP。(4分)
EF=E,∴A1E⊥面BEF,即A1E⊥面BEP。(4分)
(II)在图2中,过E点作BP的垂线,并交BP于G点,连接A1G,由(I)知A1E⊥平面BEP,∴![]() A1GE即为二面角A1-BP-E的平面角,又A1E=1,GE=
A1GE即为二面角A1-BP-E的平面角,又A1E=1,GE=![]() ,∴
,∴![]()
![]() A1GE=
A1GE=![]() ,∴
,∴![]() A1GE=
A1GE=![]() ,即所求为
,即所求为![]() 。(8分)
。(8分)


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源:2011-2012学年吉林省高二上学期期末考试数学 题型:解答题
(本题满分8分)在  中,
中,  、
、  、
、  所对的边分别是
所对的边分别是  、
、  、
、  ,其中
,其中  ,
, 
 ,求角
,求角  的大小和三角形的面积
的大小和三角形的面积  .
.
查看答案和解析>>
科目:高中数学 来源:2010年陕西省高二上学期期中考试数学理卷 题型:解答题
(本题满分8分)在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按5天一组分组统计,绘制了频率分布直方图(如图所示),已知从左到右各长方形的高的比为2∶3∶4∶6∶4∶1,第三组的频数为12,请解答下列问题:
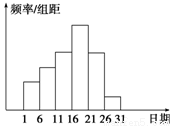
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪组获奖率高?
查看答案和解析>>
科目:高中数学 来源:2010年浙江省高二上学期10月月考数学卷 题型:解答题
(本题满分8分)
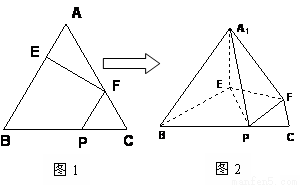
在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△AEF沿EF折起到 的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求二面角A1-BP-E的大小。
查看答案和解析>>
科目:高中数学 来源:2010年山东省北校区高二上学期第一次月考数学卷 题型:解答题
(本题满分8分)在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△AEF沿EF折起到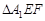 的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求二面角A1-BP-E的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com