练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图1-3-4，已知△ABC中，AB =AC，AD是BC边上的中线，CF∥BA，BF交AD于P点，交AC于E点.求证:BP2=PE·PF.

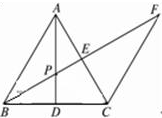
    图1-3-4

     

     

    思路解析:因为BP、PE、PF三条线段共线，找不到两个三角形，所以必须考虑等线段代换等其他方法，因为AB =AC，D是BC中点，由等腰三角形的性质知AD是BC的垂直平分线，如果我们连结PC，由线段垂直平分线的性质知PB =PC，只需证明△PEC∽△PCF，问题就能解决了.

    图1-3-5

    证明:连结PC，在△ABC中，?

    ∵AB =AC，D为BC中点，?

    ∴AD垂直平分BC.?

    ∴PB =PC.?

    ∴∠1=∠2.?

    ∵AB =AC，?

    ∴∠ABC =∠ACB.?

    ∴∠ABC-∠1=∠ACB-∠2.?

    ∴∠3=∠4.?

    ∵CF∥AB，?

    ∴∠3=∠F.?

    ∴∠4=∠F.?

    又∵∠EPC=∠CPF，?

    ∴△PCE∽△PFC.?

    ∴=.?

    ∴PC2 =PE·PF.?

    ∵PC =PB，?

    ∴PB2 =PE·PF.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

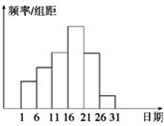    精英家教网在学校开展的综合实践活动中，某班进行了小制作评比，作品上交时间为5月1日至30日，评委会把同学们上交作品的件数按5天一组分组统计，绘制了频率分布直方图（如图所示），已知从左到右各长方形高的比为2：3：4：6：4：1，第三组的频数为12，则本次活动参加评比作品总数、上交的作品数量最多的组的作品件数依次为（　　）
    A、60、18B、60、20C、80、18D、80、30

    查看答案和解析>>

    科目：高中数学 来源： 题型：

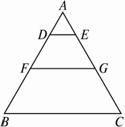
    如图1-3-14，已知△ABC中，DE∥FG∥BC，AD∶DF∶FB =2∶3∶4，求S△ADE∶S四边形DEGF∶S四边形BCGF.

    图1-3-14

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图1-3-4所示，已知D是△ABC中AB边上的一点，DE∥BC且交AC于E，EF∥AB且交BC于F，且S△ADE=1，S△EFC=4，则四边形BFED的面积等于（    ）

    图1-3-4

    A.2              B.4                C.5              D.9

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图1-3-16，已知△ABC中，DE∥FG∥BC，AD∶DF∶FB=2∶3∶4，

    求S△ADE∶S四边形DEGF∶S四边形BCGF.

    图1-3-16

    查看答案和解析>>

    同步练习册答案