
如图,已知四边形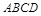 为梯形,
为梯形,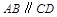 ,
,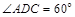 ,四边形
,四边形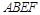 为矩形,且平面
为矩形,且平面 平面
平面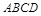 ,
, ,点
,点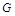 为
为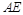 的中点.
的中点.
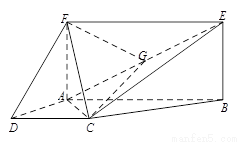
(Ⅰ)求证: 平面
平面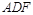 ;
;
(Ⅱ)求证:平面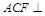 平面
平面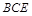 ;
;
(Ⅲ)求三棱锥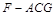 的体积.
的体积.
(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)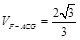 .
.
【解析】
试题分析:(Ⅰ)取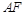 中点
中点 ,可以证明四边形
,可以证明四边形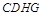 为平行四边形,即
为平行四边形,即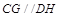 ,∴
,∴ ∥平面
∥平面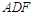 ;
;
(Ⅱ)证明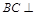 平面
平面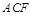 即可;(Ⅲ)改变四面体(三棱锥)的顶点,取C即可;或者利用比例.
即可;(Ⅲ)改变四面体(三棱锥)的顶点,取C即可;或者利用比例.
试题解析:(Ⅰ)取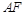 中点
中点 ,连
,连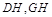 .
.

∵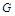 为对角线
为对角线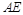 的中点,∴
的中点,∴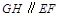 ,且
,且 ,
,
∴四边形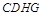 为平行四边形,即
为平行四边形,即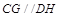 ;或者可以采用比例的方法求解.
;或者可以采用比例的方法求解.
又∵ 平面
平面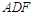 ,
, 平面
平面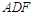 ,∴
,∴ ∥平面
∥平面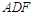 .
4分
.
4分
(Ⅱ)∵四边形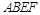 为矩形,且平面
为矩形,且平面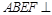 平面
平面 ,∴
,∴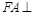 平面
平面 ,∴
,∴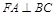 ;
;
∵四边形 为梯形,
为梯形, ,且
,且 ,∴
,∴ .
.
又在 中,
中, ,且
,且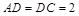 ,∴
,∴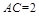 ,
,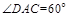 ,∴
,∴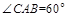 .
.
于是在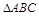 中,由
中,由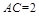 ,
,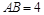 ,
,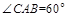 及余弦定理,得
及余弦定理,得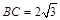 .
.
∴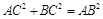 ,∴
,∴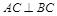 .∴
.∴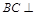 平面
平面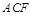 ,
,
又∵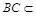 平面
平面 ,∴平面
,∴平面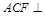 平面
平面 .
9分
.
9分
(Ⅲ)作 ,垂足为
,垂足为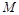 ,由平面
,由平面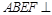 平面
平面 得
得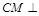 平面
平面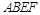 .
.
易求得 ,所以三棱锥
,所以三棱锥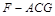 的体积为
的体积为
 . 13分.
. 13分.
【法二】连接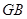 ,则
,则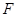 、
、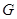 、
、 三点共线,故
三点共线,故
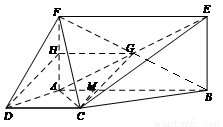
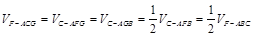
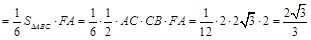
考点:线面位置关系的证明、多面体体积的计算.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
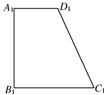
| A、3 | ||
B、3
| ||
C、6
| ||
| D、6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD.
如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD.查看答案和解析>>
科目:高中数学 来源:2009-10学年黑龙江佳一中高一第三学段考试数学 题型:解答题
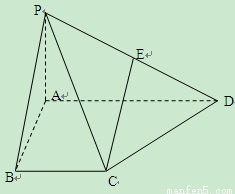
(本题满分12分)如图,已知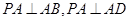 , 四边形
, 四边形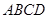 是梯形,
是梯形,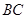 ∥
∥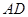 ,
, 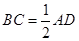 ,
,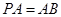 ,
, 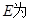
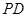 中点。
中点。
(1)求证: ∥ 平面
∥ 平面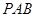 ;
;
(2)求异面直线 与
与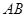 所成角的余弦值。
所成角的余弦值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com