
 已知函数f(x)=2Acos2(
已知函数f(x)=2Acos2( x+φ)-A(X∈R,A>0,|φ|<
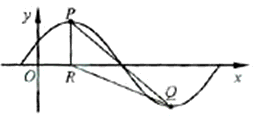
x+φ)-A(X∈R,A>0,|φ|< ),y=f(x)的部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A)
),y=f(x)的部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A) ,求△PRQ的面积.
,求△PRQ的面积. x+φ)-A=A[2cos2(
x+φ)-A=A[2cos2( x+φ)-1)=Acos(
x+φ)-1)=Acos( x+2φ),
x+2φ),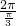 =6,
=6, +2φ)=A,cos(
+2φ)=A,cos( +2φ)=1.
+2φ)=1.
 ,所以 φ=-
,所以 φ=- . …(6分)
. …(6分) x0-
x0- =π,得 x0=4,所以Q(4,-A).
=π,得 x0=4,所以Q(4,-A). ,由余弦定理得 cos∠PRQ=
,由余弦定理得 cos∠PRQ= =
= =-
=- .
. .
. RP•RQ•sin
RP•RQ•sin =
= •A•
•A• •sin
•sin =
= =
= . …(12分)
. …(12分) x+2φ),由此求得函数的周期.再把点P(1,A)代入函数的解析式,可得cos(
x+2φ),由此求得函数的周期.再把点P(1,A)代入函数的解析式,可得cos( +2φ)=1,结合 φ的范围求得 φ的值.
+2φ)=1,结合 φ的范围求得 φ的值. ,由余弦定理求得A的值,再由 S△PRQ=
,由余弦定理求得A的值,再由 S△PRQ= RP•RQ•sin
RP•RQ•sin =
= •A•
•A• •sin
•sin ,运算求得结果.
,运算求得结果.

科目:高中数学 来源: 题型:
| 1 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com