
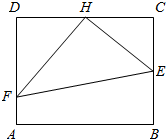
 某高校专家楼前现有一块矩形草坪ABCD,已知草坪长AB=100米,宽BC=50$\sqrt{3}$米,为了便于专家平时工作、起居,该高校计划在这块草坪内铺设三条小路HE、HF和EF,并要求H是CD的中点,点E在边BC上,点F在边AD上,且∠EHF为直角,如图所示.
某高校专家楼前现有一块矩形草坪ABCD,已知草坪长AB=100米,宽BC=50$\sqrt{3}$米,为了便于专家平时工作、起居,该高校计划在这块草坪内铺设三条小路HE、HF和EF,并要求H是CD的中点,点E在边BC上,点F在边AD上,且∠EHF为直角,如图所示.分析 (Ⅰ)要将△HEF的周长L表示成x的函数关系式,需把△HEF的三边分别用含有x的关系式来表示,从而可求.
(Ⅱ)要求铺路总费用最低,只要求△HEF的周长L的最小值即可.利用换元法,从而转化为求函数在闭区间上的最小值.
解答 解:(Ⅰ)∵在Rt△CHE中,CH=50,∠C=90°,∠CHE=x,
∴HE=$\frac{50}{cosx}$
在Rt△HDF中,HD=50,∠D=90°,∠DFH=x,
∴HF=$\frac{50}{sinx}$.
又∠EOF=90°,
∴EF=$\frac{50}{sinxcosx}$,
∴三条路的全长(即△HEF的周长)L=$\frac{50(sinx+cosx+1)}{sinxcosx}$.
当点F在点D时,这时角x最小,求得此时x=$\frac{π}{6}$;
当点E在C点时,这时角x最大,求得此时x=$\frac{π}{3}$.
故此函数的定义域为[$\frac{π}{6}$,$\frac{π}{3}$];
(Ⅱ)由题意知,要求铺路总费用最低,只要求△OEF的周长L的最小值即可.
由(Ⅰ)得L=$\frac{50(sinx+cosx+1)}{sinxcosx}$,x∈[$\frac{π}{6}$,$\frac{π}{3}$],
设sinx+cosx=t,则sinxcosx=$\frac{{t}^{2}-1}{2}$,
∴L=$\frac{100}{t-1}$
由t=sinx+cosx=$\sqrt{2}sin(x+\frac{π}{4})$,x∈[$\frac{π}{6}$,$\frac{π}{3}$],
得$\frac{\sqrt{3}+1}{2}≤t≤\sqrt{2}$,
从而$\sqrt{2}$+1≤$\frac{1}{t-1}$≤$\sqrt{3}$+1,当x=$\frac{π}{4}$,即CE=50时,Lmin=100($\sqrt{2}+1$),
所以当CE=DF=50米时,铺路总费用最低,最低总费用为96560元.
点评 本题主要考查了借助于三角函数解三角形在实际问题中的应用,考查了利用数学知识解决实际问题的能力,及推理运算的能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
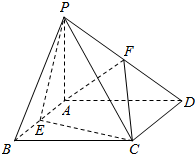 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,E、F别是AB、PD的中点.若PA=AD=CD=4.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,E、F别是AB、PD的中点.若PA=AD=CD=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
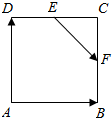
| A. | $\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AD}$ | B. | $\frac{1}{4}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$ | C. | $\frac{1}{2}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AD}$ | D. | $\frac{1}{3}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com