练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．如图，正方形ABCD中，点E是DC的中点，CF：FB=2：1，那么$\overrightarrow{EF}$=（　　）
    A．$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AD}$B．$\frac{1}{4}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$C．$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AD}$D．$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$

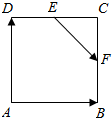
    分析 由已知可得$\overrightarrow{EF}$=$\overrightarrow{EC}$+$\overrightarrow{CF}$=$\frac{1}{2}$$\overline{DC}$+$\frac{2}{3}\overrightarrow{CB}$，进而可得答案．

    解答 解：∵正方形ABCD中，点E是DC的中点，CF：FB=2：1，
    ∴$\overrightarrow{EF}$=$\overrightarrow{EC}$+$\overrightarrow{CF}$=$\frac{1}{2}$$\overline{DC}$+$\frac{2}{3}\overrightarrow{CB}$=$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AD}$，
    故选：C

    点评 本题考查的知识点是向量的线性运算性质及几何意义，难度不大，属于基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    6．已知y=f（x）是定义在R上的单调函数，任意实数x1，x2满足x1＜x2，λ≠-1，α=$\frac{{x}_{1}+λ{x}_{2}}{1+λ}$，β=$\frac{λ{x}_{1}+{x}_{2}}{1+λ}$，若|f（x1）-f（x2）|＜|f（α）-f（β）|恒成立，则有（　　）
    A．0＜λ＜1B．λ=0C．λ＜0且λ≠-1D．λ≥1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．过抛物线y2=2px（p＞0）的焦点的一条直线与它交于P，Q两点，过点P和此抛物线顶点的直线与准线交于点M．求证直线MQ平行于此抛物线的对称轴．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

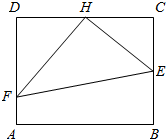    4．某高校专家楼前现有一块矩形草坪ABCD，已知草坪长AB=100米，宽BC=50$\sqrt{3}$米，为了便于专家平时工作、起居，该高校计划在这块草坪内铺设三条小路HE、HF和EF，并要求H是CD的中点，点E在边BC上，点F在边AD上，且∠EHF为直角，如图所示．
    （Ⅰ）设∠CHE=x（弧度），试将三条路的全长（即△HEF的周长）L表示成x的函数，并求出此函数的定义域；
    （Ⅱ）这三条路，每米铺设预算费用均为400元，试问如何设计才能使铺路的总费用最低？并求出最低总费用（结果保留整数）（可能用到的参考值：$\sqrt{3}$取1.732，$\sqrt{2}$取1.414）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知△ABC的三边长分别为AB=5，BC=4，AC=3，M 是AB边上的点，P是平面ABC外一点．给出下列四个命题：
    ①若PA丄平面ABC，则三棱锥P-ABC的四个面都是直角三角形；
    ②若PM丄平面ABC，且M是AB边中点，则有PA=PB=PC；
    ③若PC=5，PC丄平面ABC，则△PCM面积的最小值为$\frac{15}{2}$；
    ④若PC=5，P在平面ABC上的射影是△ABC内切圆的圆心，则点P到平面ABC的距离为$\sqrt{23}$．
    其中正确命题的序号是①②④． （把你认为正确命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．若函数f（x）=3x-1+$\frac{k}{3^x}$为偶函数，则实数k的值为$\frac{1}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．研究某设备的使用年限x与保养和维修费用y之间的关系，测得一组数据如下
    年限x（年）23456
    保养和维修费用y（万元）33.556.57
    由数据可知y与x有明显的线性相关关系，附参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2-n{\overline{x}}^{2}}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$
    （1）将表中的数据画成散点图：
    （2）试预测第7年的设备保养和维修费用．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知复数z=$\frac{2+i}{i^3}$，z的共轭复数是$\overline{z}$，则$\overline{z}$对应的点位于复平面内的（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．判断下列函数的奇偶性：
    （1）$f（x）=\frac{{{x^2}+1}}{{\sqrt{x+1}}}$；     
    （2）f（x）=|x+2|-|x-2|．

    查看答案和解析>>

    同步练习册答案