Question

3．向平面区域{（x，y）|0≤x≤2，0≤y≤2}内随机投入一点，则该点落在曲线y=$\frac{1}{x}$（x＞0）下方的概率为$\frac{1+2ln2}{4}$．

Answer 1

分析 平面区域{（x，y）|0≤x≤2，0≤y≤2}，表示正方形，面积为4，求出曲线y=$\frac{1}{x}$（x＞0）下方，在正方形内的面积，即可求出概率．

解答 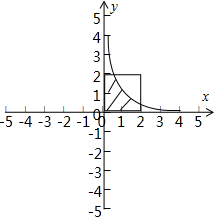解：平面区域{（x，y）|0≤x≤2，0≤y≤2}，表示正方形，面积为4，
曲线y=$\frac{1}{x}$（x＞0）下方，在正方形内的面积为$\frac{1}{2}×2$+${∫}_{\frac{1}{2}}^{2}\frac{1}{x}dx$=1+2ln2，
所以该点落在曲线y=$\frac{1}{x}$（x＞0）下方的概率为$\frac{1+2ln2}{4}$．
故答案为：$\frac{1+2ln2}{4}$．

点评 本题考查了几何概率问题，考查学生的计算能力，确定区域的面积是关键．