
已知△ABC为等边三角形,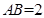 ,设点P,Q满足
,设点P,Q满足 ,
,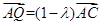 ,
,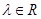 ,若
,若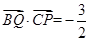 ,则
,则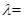 ( )
( )
A.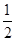 B.
B.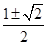 C.
C.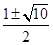 D.
D.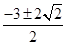
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源:福建省永定一中2011-2012学年高二下学期第一次阶段考数学文科试题 题型:013
记实数x1,x2,…,xn中的最大数为max{x1,x2…,xn},最小数为min{x1,x2,…,xn}.已知△ABC的三边边长为a、b、c(a≤b≤c),定义它的倾斜度为t=max{![]() ,
,![]() ,
,![]() }·min{
}·min{![]() ,
,![]() ,
,![]() },则“t=1”是“△ABC为等边三解形”的
},则“t=1”是“△ABC为等边三解形”的
A.充分而不必要的条件
B.必要而不充分的条件
C.充要条件
D.既不充分也不必要的条件
查看答案和解析>>
科目:高中数学 来源:北京市海淀区2012届高三下学期期中练习数学文科试题 题型:022
已知函数f(x)=![]() 则f(f(x))=________;
则f(f(x))=________;
下面三个命题中,所有真命题的序号是________.
①函数f(x)是偶函数;
②任取一个不为零的有理数T,f(x+T)=f(x)对x∈R恒成立;
③存在三个点A(x1,f(x1)),B(x2,f(x2)),C(x3,f(x3))使得△ABC为等边三角形.
查看答案和解析>>
科目:高中数学 来源:2012年北京市海淀区高考数学一模试卷(文科)(解析版) 题型:填空题
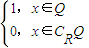 ,则f(f(x))=
,则f(f(x))= 查看答案和解析>>
科目:高中数学 来源:2012年安徽省蚌埠二中高考数学二模试卷(文科)(解析版) 题型:填空题
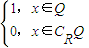 ,则f(f(x))=
,则f(f(x))= 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com