
已知函数 在
在 与
与 时都取得极值
时都取得极值
(1)求 的值与函数
的值与函数 的单调区间
的单调区间
(2)若对 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围
的取值范围
(1) 递增区间是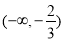 与
与 ,递减区间是
,递减区间是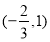 ;(2)
;(2) 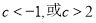 .
.
【解析】
试题分析:(1)求出f′(x),因为函数在x=-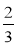
与x=1时都取得极值,所以得到f′(-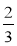 )=0且f′(1)=0联立解得a与b的值,然后把a、b的值代入求得f(x)及f′(x),然后讨论导函数的正负得到函数的增减区间;
)=0且f′(1)=0联立解得a与b的值,然后把a、b的值代入求得f(x)及f′(x),然后讨论导函数的正负得到函数的增减区间;
(2)根据(1)函数的单调性,由于x∈[-1,2]恒成立求出函数的最大值值为f(2),代入求出最大值,然后令f(2)<c2列出不等式,求出c的范围即可..
试题解析:【解析】
(1)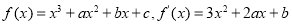 1分;
1分;
由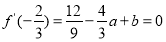 ,
,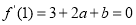 得
得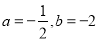 3分;
3分;
 ,函数
,函数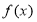 的单调区间如下表:
的单调区间如下表:
|
|
|
|
|
|
| |
|
| | |
| ? | 极大值 | ? | 极小值 | ? |
所以函数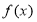 的递增区间是
的递增区间是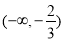 与
与 ,递减区间是
,递减区间是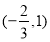 ; 6分;
; 6分;
(2) ,当
,当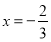 时,
时,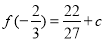
为极大值,而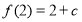 ,则
,则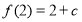 为最大值, 9分;
为最大值, 9分;
要使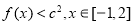 恒成立,则只需要
恒成立,则只需要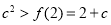 , 10分;
, 10分;
得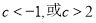 12分;
12分;
考点:1.利用导数研究函数的极值;2.函数恒成立问题;3.利用导数研究函数的单调性..


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届内蒙古包头市高二下学期期中Ⅰ理科数学试卷(解析版) 题型:选择题
下面四个判断中,正确的是( )
A.式子1+k+k2+…+kn(n∈N*)中,当n=1时式子值为1
B.式子1+k+k2+…+kn-1(n∈N*)中,当n=1时式子值为1+k
C.式子1+ +…+
+…+ (n∈N*)中,当n=1时式子值为1+
(n∈N*)中,当n=1时式子值为1+
D.设f(x)= (n∈N*),则f(k+1)=f(k)+
(n∈N*),则f(k+1)=f(k)+
查看答案和解析>>
科目:高中数学 来源:2015届内蒙古包头市高二下学期期中Ⅰ文科数学试卷(解析版) 题型:选择题
利用独立性检验来考虑两个分类变量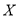 与
与 是否有关系时,通过查阅下表来确定“
是否有关系时,通过查阅下表来确定“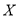 和
和 有关系”的可信度。如果
有关系”的可信度。如果 ,那么就有把握认为“
,那么就有把握认为“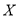 和
和 有关系”的百分比为( )
有关系”的百分比为( )
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A.25% B.95% C.5% D.97.5%
查看答案和解析>>
科目:高中数学 来源:2015届内蒙古高二下学期期末考试理科数学试卷(解析版) 题型:解答题
设进入某商场的每一位顾客购买甲种商品的概率为 ,购买乙种商品的概率为
,购买乙种商品的概率为 ,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(Ⅲ)记 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求 的分布列及期望。
的分布列及期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com