
分析 (1)由函数的图象的顶点坐标求出A,由周期求出ω,由特殊点的坐标求出φ的值,可得函数的解析式.
(2)由x的范围可求2x+$\frac{π}{6}$∈[-$\frac{5π}{6}$,$\frac{π}{6}$],利用正弦函数的性质可求其值域.
(3)利用三角函数平移变换规律可求g(x)=2sin(2x-2θ+$\frac{π}{6}$),利用正弦函数的单调性可求函数的单调递增区间,进而可得$\left\{\begin{array}{l}{kπ+θ-\frac{π}{3}≤0}\\{kπ+θ+\frac{π}{6}≥\frac{π}{4}}\end{array}\right.$,k∈Z,结合范围0<θ<$\frac{π}{2}$,可求θ的取值范围.
解答 解:(1)∵由题意可得,A=2,$\frac{2π}{ω}$=π,
∴ω=2.
∵再根据函数的图象经过点M($\frac{π}{6}$,2),可得2sin(2×$\frac{π}{6}$+φ)=2,结合|φ|<$\frac{π}{2}$,可得ω=$\frac{π}{6}$,
∴f(x)=2sin(2x+$\frac{π}{6}$).
(2)∵x∈[-$\frac{π}{2}$,0],
∴2x+$\frac{π}{6}$∈[-$\frac{5π}{6}$,$\frac{π}{6}$],
∴sin(2x+$\frac{π}{6}$)∈[-1,$\frac{1}{2}$],可得:f(x)=2sin(2x+$\frac{π}{6}$)∈[-2,1].
(3)把函数y=f(x)的图线向右平移θ(0<θ<$\frac{π}{2}$)个单位,
得到函数y=g(x)=2sin[2(x-θ)+$\frac{π}{6}$]=2sin(2x-2θ+$\frac{π}{6}$),
∴令2kπ-$\frac{π}{2}$≤2x-2θ+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z,解得:kπ+θ-$\frac{π}{3}$≤x≤kπ+θ+$\frac{π}{6}$,k∈Z,
可得函数的单调递增区间为:[kπ+θ-$\frac{π}{3}$,kπ+θ+$\frac{π}{6}$],k∈Z,
∵函数y=g(x)在[0,$\frac{π}{4}$]上是单调增函数,
∴$\left\{\begin{array}{l}{kπ+θ-\frac{π}{3}≤0}\\{kπ+θ+\frac{π}{6}≥\frac{π}{4}}\end{array}\right.$,
∴解得:$\left\{\begin{array}{l}{θ≤\frac{π}{3}-kπ}\\{θ≥\frac{π}{12}-kπ}\end{array}\right.$,k∈Z,
∵0<θ<$\frac{π}{2}$,
∴当k=0时,θ∈[$\frac{π}{12}$,$\frac{π}{3}$].
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,正弦函数的单调性和值域,考查计算能力,常考题型,题目新颖,属于基本知识的考查.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,△ABC中,AC=2,BC=4,∠ACB=90°,D、E分别是AC、AB的中点,将△ADE沿DE折起成△PDE,使面PDE⊥面BCDE,H、F分别是边PD和BE的中点,平面BCH与PE、PF分别交于点I、G.
如图,△ABC中,AC=2,BC=4,∠ACB=90°,D、E分别是AC、AB的中点,将△ADE沿DE折起成△PDE,使面PDE⊥面BCDE,H、F分别是边PD和BE的中点,平面BCH与PE、PF分别交于点I、G.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
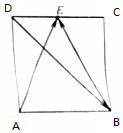
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
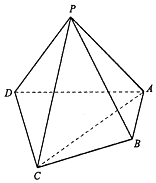 如图,在四凌锥中P-ABCD,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.
如图,在四凌锥中P-ABCD,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
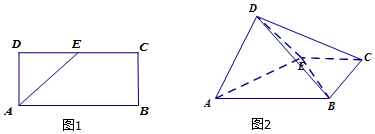
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com