
在△ABC中, 且
且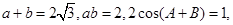
求:(1)角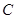 度数 (2)
度数 (2) 的长 (3)△ABC的面积
的长 (3)△ABC的面积
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:解答题
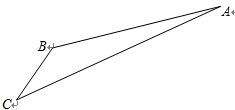
如图,旅客从某旅游区的景点 处下山至
处下山至 处有两种路径.一种是从
处有两种路径.一种是从 沿直线步行到
沿直线步行到 ,另一种从
,另一种从 沿索道乘缆车到
沿索道乘缆车到 ,然后从
,然后从 沿直线步行到
沿直线步行到 .现有甲、乙两位游客从
.现有甲、乙两位游客从 处下山,甲沿
处下山,甲沿 匀速步行,速度为
匀速步行,速度为 m/min,在甲出发2 min后,乙从
m/min,在甲出发2 min后,乙从 乘缆车到
乘缆车到 ,在
,在 处停留1 min后,再从
处停留1 min后,再从 匀速步行到
匀速步行到 . 假设缆车匀速直线运动的速度为130 m/min,山路
. 假设缆车匀速直线运动的速度为130 m/min,山路 长1260 m ,经测量,
长1260 m ,经测量, ,
, .
.
(1)求索道 的长;
的长;
(2)问乙出发后多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某人在C点测得某塔在南偏西80°的O处,塔顶A的仰角为45°,此人沿南偏东40°方向前进10米到D处,测得塔顶A的仰角为30°,求塔OA的高度?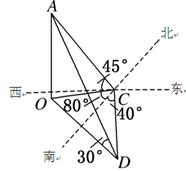
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com