
某人在C点测得某塔在南偏西80°的O处,塔顶A的仰角为45°,此人沿南偏东40°方向前进10米到D处,测得塔顶A的仰角为30°,求塔OA的高度?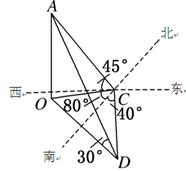
h=10,或h=-5(舍).
解析试题分析:如图,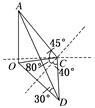
设塔高为h,在Rt△AOC中,∠ACO=45°,则OC=OA=h.…(2分)在Rt△AOD中,∠ADO=30°,则OD=h, (4分)
在△OCD中,∠OCD=120°,CD=10,由余弦定理得:OD2=OC2+CD2-2OC·CDcos∠OCD,即(h)2=h2+102-2h×10×cos120° (8分),
∴h2-5h-50=0,解得h=10,或h=-5(舍). 12分
考点:正弦定理、余弦定理的应用。
点评:典型题,本题综合考查正弦定理、余弦定理的应用,本题解答结合图形,在不同的几个三角形中,灵活运用正弦定理或余弦定理,反映应用数学知识的灵活性。解决“追击问题”,测量高度或距离问题,准确绘制几何图形,明确边、角,是解题的关键。


 科学实验活动册系列答案
科学实验活动册系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com