
【题目】(20)(本小题满分13分)
已知函数![]() ,
,![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)令![]() ,讨论
,讨论![]() 的单调性并判断有无极值,有极值时求出极值.
的单调性并判断有无极值,有极值时求出极值.
【答案】(Ⅰ)![]() .
.
(Ⅱ)综上所述:
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
函数![]() 有极小值,极小值是
有极小值,极小值是![]() ;
;
当![]() 时,函数
时,函数![]() 在
在![]() 和
和![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减,函数
上单调递减,函数![]() 有极大值,也有极小值,
有极大值,也有极小值,
极大值是![]()
极小值是![]() ;
;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,无极值;
上单调递增,无极值;
当![]() 时,函数
时,函数![]() 在
在![]() 和
和![]() 上单调递增,
上单调递增,
在![]() 上单调递减,函数
上单调递减,函数![]() 有极大值,也有极小值,
有极大值,也有极小值,
极大值是![]() ;
;
极小值是![]() .
.
【解析】解:(Ⅰ)由题意![]()
又![]() ,
,
所以![]() ,
,
因此 曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为
![]() ,
,
即 ![]() .
.
(Ⅱ)由题意得 ![]() ,
,
因为![]()
![]()
![]() ,
,
令![]()
则![]()
所以![]() 在
在![]() 上单调递增.
上单调递增.
所以 当![]() 时,
时,![]() 单调递减,
单调递减,
当![]() 时,
时,![]()
(1)当![]() 时,
时,![]()
![]()
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
所以 当![]() 时
时![]() 取得极小值,极小值是
取得极小值,极小值是 ![]() ;
;
(2)当![]() 时,
时,![]()
由 ![]() 得
得 ![]() ,
,![]()
①当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
所以 当![]() 时
时![]() 取得极大值.
取得极大值.
极大值为![]() ,
,
当![]() 时
时![]() 取到极小值,极小值是
取到极小值,极小值是 ![]() ;
;
②当![]() 时,
时,![]() ,
,
所以 当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增,无极值;
上单调递增,无极值;
③当![]() 时,
时,![]()
所以 当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
所以 当![]() 时
时![]() 取得极大值,极大值是
取得极大值,极大值是![]() ;
;
当![]() 时
时![]() 取得极小值.
取得极小值.
极小值是![]() .
.
综上所述:
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
函数![]() 有极小值,极小值是
有极小值,极小值是![]() ;
;
当![]() 时,函数
时,函数![]() 在
在![]() 和
和![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减,函数
上单调递减,函数![]() 有极大值,也有极小值,
有极大值,也有极小值,
极大值是![]()
极小值是![]() ;
;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,无极值;
上单调递增,无极值;
当![]() 时,函数
时,函数![]() 在
在![]() 和
和![]() 上单调递增,
上单调递增,
在![]() 上单调递减,函数
上单调递减,函数![]() 有极大值,也有极小值,
有极大值,也有极小值,
极大值是![]() ;
;
极小值是![]() .
.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,BC⊥平面APC,AB=2 ![]() ,AP=PC=CB=2.
,AP=PC=CB=2. 
(1)求证:AP⊥平面PBC;
(2)求二面角P﹣AB﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】河道上有一座圆拱桥,在正常水位时,拱圈最高点距水面9m,拱圈内水面宽22m.一条船在水面以上部分高6.5m,船顶部宽4m,故通行无阻.近日水位暴涨了2.7m,为此,必须加重舰载,降低船身,才能通过桥洞.试问船身至少应该降低多少?(精确到0.01,参考数据: ![]() )
) 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:在四棱锥P﹣ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且PA=AB=2.
(Ⅰ)证明:BC⊥平面AMN;
(Ⅱ)求三棱锥N﹣AMC的体积;
(Ⅲ)在线段PD上是否存在一点E,使得NM∥平面ACE;若存在,求出PE的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
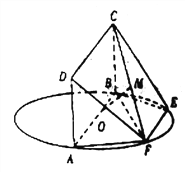
【题目】如图所示, ![]() 为圆
为圆![]() 的直径,点
的直径,点![]() ,
, ![]() 在圆
在圆![]() 上,
上, ![]() ,矩形
,矩形![]() 所在的平面和圆
所在的平面和圆![]() 所在的平面互相垂直,且
所在的平面互相垂直,且![]() ,
, ![]() ,
, ![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)设![]() 的中点为
的中点为![]() ,求三棱锥
,求三棱锥![]() 的体积
的体积![]() 与多面体
与多面体![]() 的体积
的体积![]() 之比的值.
之比的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是公差为1的等差数列,a1 , a5 , a25成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=3 ![]() +an , 求数列{bn}的前n项和Tn .
+an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人进行乒乓球决赛,比赛采取七局四胜制.现在的情形是甲胜3局,乙胜2局.若两人胜每局的概率相同,则甲获得冠军的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com