
设f(x)是定义在R上以2为周期的偶函数,已知x∈(0,1)时,f(x)=lo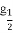 (1-x),则函数f(x)在(1,2)上( )
(1-x),则函数f(x)在(1,2)上( )
(A)是增函数,且f(x)<0
(B)是增函数,且f(x)>0
(C)是减函数,且f(x)<0
(D)是减函数,且f(x)>0
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学文二轮专题复习与测试选修4-5不等式选讲 练习卷(解析版) 题型:填空题
已知对于任意非零实数m,不等式|2m-1|+|1-m|≥|m|(|x-1|-|2x+3|)恒成立,则实数x的取值范围为____________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文二轮专题复习与测试解答题保分训练练习卷(解析版) 题型:解答题
已知数列{an}的相邻两项an,an+1是关于x的方程x2-2nx+bn=0的两根,且a1=1.
(1)求证:数列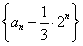 是等比数列;
是等比数列;
(2)求数列{an}的前n项和Sn;
(3)设函数f(n)=bn-t·Sn(n∈N*),若f(n)>0对任意的n∈N*都成立,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(四)第二章第一节练习卷(解析版) 题型:选择题
函数f(x)=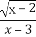 +lg
+lg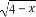 的定义域是( )
的定义域是( )
(A)(2,4) (B)(3,4)
(C)(2,3)∪(3,4] (D)[2,3)∪(3,4)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(六)第二章第三节练习卷(解析版) 题型:填空题
函数y=f(x)(x∈R)有下列命题:
①在同一坐标系中,y=f(x+1)与y=f(-x+1)的图象关于直线x=1对称;
②若f(2-x)=f(x),则函数y=f(x)的图象关于直线x=1对称;
③若f(x-1)=f(x+1),则函数y=f(x)是周期函数,且2是一个周期;
④若f(2-x)=-f(x),则函数y=f(x)的图象关于(1,0)对称,其中正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(六)第二章第三节练习卷(解析版) 题型:选择题
已知f(x)是周期为2的奇函数,当0<x<1时,f(x)=lgx,设a=f( ),b=f(
),b=f( ),c=f(
),c=f( ),则( )
),则( )
(A)c<a<b (B)a<b<c (C)b<a<c (D)c<b<a
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(八)第二章第五节练习卷(解析版) 题型:填空题
已知f(3x)=4xlog23+233,则f(2)+f(4)+f(8)+…+f(28)的值是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(五)第二章第二节练习卷(解析版) 题型:填空题
对a,b∈R,记max(a,b)=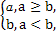 函数f(x)=max(|x+1|,-x2+1)的最小值是 .
函数f(x)=max(|x+1|,-x2+1)的最小值是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(九)第二章第六节练习卷(解析版) 题型:选择题
已知函数y=x2-2x+3在闭区间[0,m]上有最大值3,最小值2,则m的取值范围是( )
(A)[1,+∞) (B)[0,2]
(C)[1,2] (D)(-∞,2]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com