
已知以点C 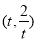 (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y-4=0与圆C交于点M、N,若|OM|=|ON|,求圆C的方程;
(3)在(2)的条件下,设P、Q分别是直线l:x+y+2=0和圆C的动点,求|PB|+|PQ|的最小值及此时点P的坐标.
(1)见解析(2)(x-2)2+(y-1)2=5(3)2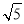 ,坐标为
,坐标为
【解析】(1)证明 由题设知,圆C的方程为(x-t)2+ 2=t2+
2=t2+ ,
,
化简得x2-2tx+y2-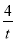 y=0,
y=0,
当y=0时,x=0或2t,则A(2t,0);
当x=0时,y=0或 ,则B
,则B  ,
,
∴S△AOB=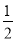 |OA|·|OB|=
|OA|·|OB|=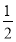 |2t|·
|2t|· =4为定值.
=4为定值.
(2)解 ∵|OM|=|ON|,则原点O在MN的中垂线上,设MN的中点为H,则CH⊥MN,
∴C、H、O三点共线,则直线OC的斜率
k=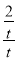 =
=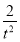 =
=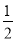 ,∴t=2或t=-2.
,∴t=2或t=-2.
∴圆心为C(2,1)或C(-2,-1),
∴圆C的方程为(x-2)2+(y-1)2=5或(x+2)2+(y+1)2=5由于当圆方程为(x+2)2+(y+1)2=5时,直线2x+y-4=0到圆心的距离d>r,此时不满足直线与圆相交,故舍去,
∴圆C的方程为(x-2)2+(y-1)2=5.
(3)解 点B(0,2)关于直线x+y+2=0的对称点B′(-4,-2),则|PB|+|PQ|=|PB′|+|PQ|≥|B′Q|,
又B′到圆上点Q的最短距离为
|B′C|-r=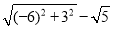 =3
=3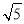 -
-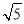 =2
=2 .
.
所以|PB|+|PQ|的最小值为2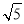 ,直线B′C的方程为y=
,直线B′C的方程为y= x,则直线B′C与直线x+y+2=0的交点P的坐标为
x,则直线B′C与直线x+y+2=0的交点P的坐标为 .
.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(解析版) 题型:填空题
关于x的方程x3-3x2-a=0有三个不同的实数解,则实数a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练1练习卷(解析版) 题型:解答题
已知函数f(x)=loga(x+1)(a>1),若函数y=g(x)的图象上任意一点P关于原点对称的点Q的轨迹恰好是函数f(x)的图象.
(1)写出函数g(x)的解析式;
(2)当x∈[0,1)时总有f(x)+g(x)≥m成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习7-2随机变量及其分布练习卷(解析版) 题型:选择题
若随机变量X的概率分布密度函数是φμ,σ(x)= (x∈R),则E(2X-1)=( ).
(x∈R),则E(2X-1)=( ).
A.-1 B.-2
C.-4 D.-5
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习6-2椭圆、双曲线、抛物线练习卷(解析版) 题型:选择题
已知直线l交椭圆4x2+5y2=80于M,N两点,椭圆与y轴的正半轴交于B点,若△BMN的重心恰好落在椭圆的右焦点上,则直线l的方程是( ).
A.6x-5y-28=0 B.6x+5y-28=0
C.5x+6y-28=0 D.5x-6y-28=0
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习6-1直线与圆练习卷(解析版) 题型:填空题
已知直线 ax+by=1(a,b是实数)与圆O:x2+y2=1(O是坐标原点)相交于A,B两点,且△AOB是直角三角形,点P(a,b)是以点M(0,1)为圆心的圆M上的任意一点,则圆M的面积的最小值为________.
ax+by=1(a,b是实数)与圆O:x2+y2=1(O是坐标原点)相交于A,B两点,且△AOB是直角三角形,点P(a,b)是以点M(0,1)为圆心的圆M上的任意一点,则圆M的面积的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习5-2空间向量与立体几何练习卷(解析版) 题型:填空题
正四棱锥S-ABCD中,O为顶点在底面上的射影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC所成的角是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习4-2数列求和与数列的综合应用练习卷(解析版) 题型:解答题
已知Sn是数列{an}的前n项和,且an=Sn-1+2(n≥2),a1=2.
(1)求数列{an}的通项公式.
(2)设bn=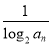 ,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得
,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得
对于任意的正整数n,有Tn>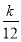 恒成立?若存在,求出k的值;若不存在,说明理由.
恒成立?若存在,求出k的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习2-2导数及其应用练习卷(解析版) 题型:解答题
甲方是一农场,乙方是一工厂.由于乙方生产需占用甲方的资源,因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入,在乙方不赔付甲方的情况下,乙方的年利润x(元)与年产量t(吨)满足函数关系x=2 000 .若乙方每生产一吨产品必须赔付甲方S元(以下称S为赔付价格).
.若乙方每生产一吨产品必须赔付甲方S元(以下称S为赔付价格).
(1)将乙方的年利润w(元)表示为年产量t(吨)的函数,并求出乙方获得最大利润的年产量;
(2)甲方每年受乙方生产影响的经济损失金额y=0.002t2(元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格S是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com