练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝loga(x＋1)(a>1)，若函数y＝g(x)的图象上任意一点P关于原点对称的点Q的轨迹恰好是函数f(x)的图象．

    (1)写出函数g(x)的解析式；

    (2)当x∈[0,1)时总有f(x)＋g(x)≥m成立，求m的取值范围．

     

    （1）y＝－loga(1－x)(x<1)（2）(－∞，0]

    【解析】(1)设P(x，y)为g(x)图象上任意一点，则Q(－x，－y)是点P关于原点的对称点，因为Q(－x，－y)在f(x)的图象上，所以－y＝loga(－x＋1)，

    即y＝－loga(1－x)(x<1)．

    (2)f(x)＋g(x)≥m，

    即loga ≥m.

    设F(x)＝loga ，x∈[0,1)．

    由题意知，只要F(x)min≥m即可．

    因为F(x)在[0,1)上是增函数，所以F(x)min＝F(0)＝0.

    故m的取值范围是(－∞，0]．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练x4-1练习卷（解析版） 题型：填空题

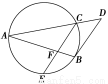
    如图，已知AB和AC是圆的两条弦，过点B作圆的切线与AC的延长线相交于点D.过点C作BD的平行线与圆相交于点E，与AB相交于点F，AF＝3，FB＝1，EF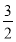＝，则线段CD的长为________．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练4练习卷（解析版） 题型：选择题

    已知函数y＝f(x)是定义在R上的奇函数，且当x<0时，不等式f(x)＋xf′(x)<0成立，若a＝30.3f(30.3)，b＝logπ3f(logπ3)，c＝log3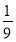f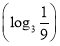，则a，b，c间的大小关系是(　　)．

    A．a>b>c B．c>b>a

    C．c>a>b D．a>c>b

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练2练习卷（解析版） 题型：解答题

    某分公司经销某种品牌产品，每件产品的成本为3元，并且每件产品需向总公司交a元(3≤a≤5)的管理费，预计当每件产品的售价为x元(9≤x≤11)时，一年的销售量为(12－x)2万件．

    (1)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式；

    (2)当每件产品的售价为多少元时，分公司一年的利润L最大？并求出L的最大值Q(a)．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练2练习卷（解析版） 题型：选择题

    函数f(x)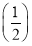＝x－sin x在区间[0,2π]上的零点个数为(　　)．

    A．1 B．2 C．3 D．4

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练1练习卷（解析版） 题型：选择题

    已知x，y为正实数，则(　　)．

    A．2lg x＋lg y＝2lg x＋2lg y B．2lg(x＋y)＝2lg x·2lg y

    C．2lg x·lg y＝2lg x＋2lg y D．2lg(xy)＝2lg x·2lg y

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习7-2随机变量及其分布练习卷（解析版） 题型：填空题

    随机变量ξ的分布列如下：

    ξ

    －1

    0

    1

    P

    a

    b

    c

    其中a，b，c成等差数列．若Eξ＝，则Dξ的值是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习6-1直线与圆练习卷（解析版） 题型：解答题

    已知以点C 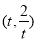(t∈R，t≠0)为圆心的圆与x轴交于点O、A，与y轴交于点O、B，其中O为原点．

    (1)求证：△AOB的面积为定值；

    (2)设直线2x＋y－4＝0与圆C交于点M、N，若|OM|＝|ON|，求圆C的方程；

    (3)在(2)的条件下，设P、Q分别是直线l：x＋y＋2＝0和圆C的动点，求|PB|＋|PQ|的最小值及此时点P的坐标．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习4-1等差数列与等比数列练习卷（解析版） 题型：填空题

    设数列{an}是公差不为零的等差数列，Sn是数列{an}的前n项和，且S＝9S2，S4＝4S2，则数列{an}的通项公式为________．

     

    查看答案和解析>>

    同步练习册答案