
����Ŀ���ڹ��ҡ����ڴ�ҵ�����ڴ��¡�ս���£�ij��ҵ�����Ӵ��ij�ֲ�Ʒ���о�Ͷ��.Ϊ�˶����з��IJ�Ʒ���к������ۣ����ò�Ʒ�������ⶨ�ļ۸��������õ�һ�������������ʾ��
�����۸� |
|
|
|
|
|
|
��Ʒ���� |
|
|
|
|
|
|
��֪����![]() ��
��![]() ����������ع�ϵ�����мס��ҡ�����λͬѧͨ��������ûع�ֱ�߷��̷ֱ�Ϊ����/span>
����������ع�ϵ�����мס��ҡ�����λͬѧͨ��������ûع�ֱ�߷��̷ֱ�Ϊ����/span>![]() ����
����![]() ����
����![]() ���������ҽ���һλͬѧ�ļ���������ȷ��.
���������ҽ���һλͬѧ�ļ���������ȷ��.
��1�����ж�˭�ļ�������ȷ����ع鷽�̡�
��2���������Իع鷽�̵õ��Ĺ��������������ݵ�������1����ü�������ǡ��������ݡ�.�ִӼ�������������ȡ3�������������ݡ��ĸ���![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
���𰸡�(1) ��ͬѧ��ȷ�� ![]() (2)������
(2)������
��������
��1���ɱ���![]() ��
��![]() �������Ը���ع�ϵ����֪�״���������������
�������Ը���ع�ϵ����֪�״���������������![]() ���飬�ɵ�����ȷ��
���飬�ɵ�����ȷ��
��2���ɼ���ɵá��������ݡ�����3�����ɵ�x��ȡֵ���ֱ�������ʣ�����д���ֲ��к�������
��1����֪����![]() ��
��![]() �������Ը���ع�ϵ���ʼײ��ԣ�
�������Ը���ع�ϵ���ʼײ��ԣ�
![]() ��
��![]() �����������ع鷽�̣���֤��ͬѧ��ȷ��
�����������ع鷽�̣���֤��ͬѧ��ȷ��
�ʻع鷽��Ϊ��![]() ��
��
��2��
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
���������� ���ĸ���![]() ȡֵΪ��
ȡֵΪ��![]() ��
��
![]() ,
,![]() ,
,
![]() ,
,![]()
���ǡ��������ݡ��ĸ���![]() �ķֲ��У�
�ķֲ��У�
|
|
|
|
|
|
|
|
|
|
��ѧ����![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
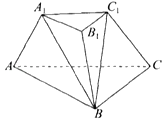
����Ŀ����ͼ��������̨ABC��A1B1C1�У�����ABC�DZ߳�Ϊ2�ĵȱ������Σ��ϡ��µ�������֮��Ϊ1��4������A1ABB1�͵���ABC������A1A��A1B1����AA1B��90����
��1��ƽ��A1C1B��ƽ��ABC��l��֤����A1C1��l��
��2����ƽ��A1C1B��ƽ��ABC���ɶ���ǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��ǰn���Ϊ
��ǰn���Ϊ![]() ������
������![]() (
(![]() )������
)������![]() Ϊ�Ȳ����У���
Ϊ�Ȳ����У���![]() ��
��![]() ��
��
��1��������![]() ��
��![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2����![]() ����
Ϊ����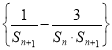 ��ǰn��ͣ������㲻��ʽ
��ǰn��ͣ������㲻��ʽ![]() ��n�����ֵ��
��n�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ֻ����ռ���ʹ���ֻ�������Ϊ�������ճ������һ���֣��ܶ������߶��ֻ�����������Խ��Խ��.ijͨ�Ź�˾Ϊ�˸��õ����������߶��������������Ƴ�һ��������.��ͨ�Ź�˾ѡ���˿ڹ�ģ�൱��![]() �����в��ò�ͬ�Ķ��۷�����Ϊ�Ե㣬����һ���µ�ͳ�ƣ����ָ��������Ķ���:
�����в��ò�ͬ�Ķ��۷�����Ϊ�Ե㣬����һ���µ�ͳ�ƣ����ָ��������Ķ���: ![]() (��λ:Ԫ/��)����������
(��λ:Ԫ/��)����������![]() (��λ:����)�Ĺ�ϵ���:
(��λ:����)�Ĺ�ϵ���:
����x��Ԫ/�£� | 20 | 30 | 50 | 60 |
�����ˣ�40�����£� | 10 | 15 | 7 | 8 |
�������ˣ�40���Լ�40�����ϣ� | 20 | 15 | 3 | 2 |
����������y�����ˣ� | 30 | 30 | 10 | 10 |
�����ݱ��е����ݣ��������Իع�ģ�����![]() ��
��![]() �Ĺ�ϵ�����
�Ĺ�ϵ�����![]() ����
����![]() �Ļع鷽��;������
�Ļع鷽��;������![]() Ԫ/�µ����������ж����˹���?
Ԫ/�µ����������ж����˹���?
��������![]() Ԫ/������(������
Ԫ/������(������![]() Ԫ)����������Ϊ�ͼ���������
Ԫ)����������Ϊ�ͼ���������![]() Ԫ����(����
Ԫ����(����![]() Ԫ)����������Ϊ���������������ö����Լ���֪ʶ����д��������������ͨ������˵���Ƿ����ڷ�����ĸ��ʲ�����
Ԫ)����������Ϊ���������������ö����Լ���֪ʶ����д��������������ͨ������˵���Ƿ����ڷ�����ĸ��ʲ�����![]() ��ǰ���£���Ϊ�����˵������С���������۸�ߵ��й�?
��ǰ���£���Ϊ�����˵������С���������۸�ߵ��й�?
����x��Ԫ/�£� | С��50Ԫ | ���ڻ����50Ԫ | �ܼ� |
�����ˣ�40�����£� | |||
�������ˣ�40���Լ�40�����ϣ� | |||
�ܼ� |
�ο���ʽ������![]()
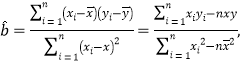
![]()
![]() ����
����![]()
�ο����ݣ�
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijʡȷ����2021�꿪ʼ���߿����á�![]() ����ģʽ��ȡ�������ֿƣ�����3���������ġ���ѧ��Ӣ�Ϊ�ؿ���Ŀ����1����ʾ����������ʷ����ѡһ�ţ���2�����Ǵ������ѧ��������������ѡ�����ţ��������ſ��Կ�Ŀ.ij���дӸ�һ�꼶2000��ѧ��������Ů��900�ˣ��У����÷ֲ�����ķ�����ȡ
����ģʽ��ȡ�������ֿƣ�����3���������ġ���ѧ��Ӣ�Ϊ�ؿ���Ŀ����1����ʾ����������ʷ����ѡһ�ţ���2�����Ǵ������ѧ��������������ѡ�����ţ��������ſ��Կ�Ŀ.ij���дӸ�һ�꼶2000��ѧ��������Ů��900�ˣ��У����÷ֲ�����ķ�����ȡ![]() ��ѧ�����е���.
��ѧ�����е���.
��1����֪��ȡ��![]() ��ѧ���к�����110�ˣ���
��ѧ���к�����110�ˣ���![]() ��ֵ����ȡ����Ů��������
��ֵ����ȡ����Ů��������
��2��ѧУ�ƻ��ڸ߶���ѧ�ڿ���ѡ���еġ��������͡���ʷ��������Ŀ��Ϊ���˽�ѧ������������Ŀ��ѡ����������ڣ�1���������³�ȡ����![]() ��ѧ�������ʾ����飨�ٶ�ÿ��ѧ������������Ŀ�б���ѡ��һ����Ŀ��ֻ��ѡ��һ����Ŀ��.�±��Ǹ��ݵ������õ���
��ѧ�������ʾ����飨�ٶ�ÿ��ѧ������������Ŀ�б���ѡ��һ����Ŀ��ֻ��ѡ��һ����Ŀ��.�±��Ǹ��ݵ������õ���![]() ���������뽫�������������������ж��Ƿ���
���������뽫�������������������ж��Ƿ���![]() �İ�����Ϊѡ���Ŀ���Ա��йأ�˵��������ɣ�
�İ�����Ϊѡ���Ŀ���Ա��йأ�˵��������ɣ�
�Ա� | ѡ������ | ѡ����ʷ | �ܼ� |
���� | 50 | ||
�� | 30 | ||
�ܼ� |
��3���ڣ�2���������£��ӳ�ȡ��ѡ����������ѧ���а��ֲ������ȡ6�ˣ��ٴ���6��ѧ���г�ȡ2�ˣ��ԡ���������ѡ�������������˽⣬��2����������1��Ů���ĸ���.
�ο���ʽ��![]() ������
������![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��һ������Ϊ
��һ������Ϊ![]() ���϶���Ϊ
���϶���Ϊ![]() ��ԭ��O��ֱ��
��ԭ��O��ֱ��![]() �ľ���Ϊ
�ľ���Ϊ![]() .
.
(1)����ԲC�ı����̣�
(2)����T��Բ![]() �ϣ���AΪ��Բ���Ҷ��㣬�Ƿ���ڹ���A��ֱ��l����ԲC�ڵ�B�����ڵ�A����ʹ��
�ϣ���AΪ��Բ���Ҷ��㣬�Ƿ���ڹ���A��ֱ��l����ԲC�ڵ�B�����ڵ�A����ʹ��![]() �����������ڣ����ֱ��l�ķ��̣��������ڣ���˵������.
�����������ڣ����ֱ��l�ķ��̣��������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ������Բ�ϴ���һ��
������Բ�ϴ���һ��![]() ������
������![]() .
.
��1������Բ![]() �ı����̣�
�ı����̣�
��2������Բ![]() �ҽ���
�ҽ���![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() ���ڲ�ͬ������
���ڲ�ͬ������![]() ����
����![]() ������Բ�İ뾶�����ֵ.
������Բ�İ뾶�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ������һ����ͼ��ʾ��Բ���������ޣ����µ��漰����ĺ�Ȳ��ƣ������������Ϊ![]() ,��Բ���ĸ߶�Ϊ
,��Բ���ĸ߶�Ϊ![]() ������뾶Ϊ
������뾶Ϊ![]() ����
����![]() ,�����������������ý����������йأ���֪���������������Ϊ
,�����������������ý����������йأ���֪���������������Ϊ![]() Ԫ
Ԫ![]() �����������µ����������þ�Ϊ
�����������µ����������þ�Ϊ![]() Ԫ
Ԫ![]() Ϊ����)��
����)��
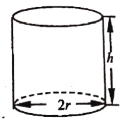
��1��д���������������![]() (Ԫ)����
(Ԫ)����![]() �ĺ�������ʽ�������䶨����
�ĺ�������ʽ�������䶨����
��2��������������������ʱ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Բ![]() Ϊ���ҽ���,
Ϊ���ҽ���,![]() Ϊ����˵�,���᳤Ϊ4,����Ϊ
Ϊ����˵�,���᳤Ϊ4,����Ϊ![]() ,��
,��![]() ,
,![]() �����Ϊ
�����Ϊ![]() .
.
(��)����Բ![]() �ķ���
�ķ���
(��)�趯ֱ��![]() ��Բ
��Բ![]() ���ҽ���һ��������
���ҽ���һ��������![]() ,����ֱ��
,����ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() .��̽��:������ƽ�����Ƿ���ڶ���
.��̽��:������ƽ�����Ƿ���ڶ���![]() ,ʹ����
,ʹ����![]() Ϊֱ����Բ�����
Ϊֱ����Բ�����![]() ?�����������
?�����������![]() ������,��������.��˵������.
������,��������.��˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com