
ΓΨΧβΡΩΓΩœ÷‘Ύ»ΥΟ«ΕΦΉΔ÷ΊΕΆΝΕ…μΧεΘ§Το≥ΒΜρ≤Ϋ––…œœ¬ΑύΒΡ»Υ‘Ϋά¥‘ΫΕύΘ§Ρ≥―ß–ΘΦΉΓΔ““ΝΫΟϊΫΧ ΠΟΩΧλΩ…≤…”Ο≤Ϋ––ΓΔΤο≥ΒΓΔΩΣ≥Β»ΐ÷÷ΖΫ Ϋ…œœ¬ΑύΘ§≤Ϋ––ΒΫ―ß–ΘΥυ”Ο ±ΦδΈΣ1–Γ ±Θ§Το≥ΒΒΫ―ß–ΘΥυ”Ο ±ΦδΈΣ0.5–Γ ±Θ§ΩΣ≥ΒΒΫ―ß–ΘΥυ”Ο ±ΦδΈΣ0.1–Γ ±Θ§ΦΉΓΔ““ΝΫ»Υ…œœ¬ΑύΖΫ ΫΜΞ≤Μ”Αœλ.…ηΦΉΓΔ““≤Ϋ––ΒΡΗ≈¬ Ζ÷±πΈΣ![]() ΓΔ
ΓΔ![]() Θ§Το≥ΒΒΡΗ≈¬ Ζ÷±πΈΣ
Θ§Το≥ΒΒΡΗ≈¬ Ζ÷±πΈΣ![]() ΓΔ
ΓΔ![]() .
.
(1) «σΦΉΓΔ““ΝΫ»ΥΒΫ―ß–ΘΥυ”Ο ±ΦδœύΆ§ΒΡΗ≈¬ ΘΜ
(2) …ηΦΉΓΔ““ΝΫ»ΥΒΫ―ß–ΘΥυ”Ο ±ΦδΚΆΈΣΥφΜζ±δΝΩ![]() Θ§«σ
Θ§«σ![]() ΒΡΖ÷≤ΦΝ–ΦΑ ΐ―ßΤΎΆϊ.
ΒΡΖ÷≤ΦΝ–ΦΑ ΐ―ßΤΎΆϊ.
ΓΨ¥πΑΗΓΩΦϊΫβΈω
ΓΨΫβΈωΓΩΘ®1Θ©”…Χβ“βΘ§ΒΟΦΉΓΔ““ΝΫ»ΥΩΣ≥ΒΒΡΗ≈¬ Ζ÷±πΈΣ![]() Θ§................2Ζ÷
Θ§................2Ζ÷
Φ«ΦΉΓΔ““ΝΫ»ΥΒΫ―ß–ΘΥυ”Ο ±ΦδœύΆ§ΈΣ ¬ΦΰAΘ§
‘ρ![]()
Υυ“‘ΦΉΓΔ““ΝΫ»ΥΒΫ―ß–ΘΥυ”Ο ±ΦδœύΆ§ΒΡΗ≈¬ ΈΣ![]() . Γ≠Γ≠6Ζ÷
. Γ≠Γ≠6Ζ÷
Θ®2Θ©![]()
‘ρ![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() . ................10Ζ÷
. ................10Ζ÷
Υυ“‘ΦΉΓΔ““ΝΫ»ΥΒΫ―ß–ΘΥυ”Ο ±Φδ÷°ΚΆΒΡΖ÷≤ΦΝ–ΈΣ
X | 0.2 | 0.6 | 1.0 | 1.1 | 1.5 | 2 |
P |
|
|
|
|
|
|
Υυ“‘![]()
![]() Θ®–Γ ±Θ©. Γ≠Γ≠12Ζ÷
Θ®–Γ ±Θ©. Γ≠Γ≠12Ζ÷


 ΩΤ―ß Β―ιΜνΕ·≤αœΒΝ–¥πΑΗ
ΩΤ―ß Β―ιΜνΕ·≤αœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥÷–―ßΒς≤ιΝΥΡ≥Αύ»Ϊ≤Ω50ΟϊΆ§―ß≤ΈΦ” ιΖ®…γΆ≈ΚΆ―ίΫ≤…γΆ≈ΒΡ«ιΩωΘ§ ΐΨί»γœ¬±μΘΚΘ®ΒΞΈΜΘΚ»ΥΘ©
≤ΈΦ” ιΖ®…γΆ≈ | Έ¥≤ΈΦ” ιΖ®…γΆ≈ | |
≤ΈΦ”―ίΫ≤…γΆ≈ | 8 | 6 |
Έ¥≤ΈΦ”―ίΫ≤…γΆ≈ | 6 | 30 |
Θ®IΘ©¥”ΗΟΑύΥφΜζ―Γ1ΟϊΆ§―ßΘ§«σΗΟΆ§―ß÷Ν…Ό≤ΈΦ”…œ ω“ΜΗω…γΆ≈ΒΡΗ≈¬ ΘΜ
Θ®IIΘ©‘ΎΦ»≤ΈΦ” ιΖ®…γΆ≈”÷≤ΈΦ”―ίΫ≤…γΆ≈ΒΡ8ΟϊΆ§―ß÷–Θ§”–5ΟϊΡ–Ά§―ßA1Θ§A2Θ§A3Θ§A4Θ§A5Θ§3Οϊ≈°Ά§―ßB1Θ§B2Θ§B3Θ§œ÷¥”’β5ΟϊΡ–Ά§―ßΚΆ3Οϊ≈°Ά§―ß÷–ΗςΥφΜζ―Γ1»ΥΘ§«σA1±Μ―Γ÷–«“B1Έ¥±Μ―Γ÷–ΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ―Γ–ό4-4ΘΚΉχ±ξœΒ”κ≤Έ ΐΖΫ≥Χ
‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§«ζœΏ
÷–Θ§«ζœΏ![]() ΘΚ
ΘΚ![]() Θ§«ζœΏ
Θ§«ζœΏ![]() ΘΚ
ΘΚ![]() Θ®
Θ®![]() ΈΣ≤Έ ΐΘ©Θ§ “‘Ήχ±ξ‘≠Βψ
ΈΣ≤Έ ΐΘ©Θ§ “‘Ήχ±ξ‘≠Βψ![]() ΈΣΦΪΒψΘ§
ΈΣΦΪΒψΘ§![]() ÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ°
÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ°
Θ®1Θ©«σ«ζœΏ![]() Θ§
Θ§![]() ΒΡΦΪΉχ±ξΖΫ≥ΧΘΜ
ΒΡΦΪΉχ±ξΖΫ≥ΧΘΜ
Θ®2Θ©»τ…δœΏ![]() ΘΚ
ΘΚ![]() Θ®
Θ®![]() Θ©Ζ÷±πΫΜ
Θ©Ζ÷±πΫΜ![]() Θ§
Θ§![]() ”Ύ
”Ύ![]() ΝΫΒψΘ§ «σ
ΝΫΒψΘ§ «σ![]() ΒΡΉν¥σ÷ΒΘ°
ΒΡΉν¥σ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τmΗω≤Μ»ΪœύΒ»ΒΡ’ΐ ΐa1 Θ§ a2 Θ§ Γ≠am“ά¥ΈΈß≥…“ΜΗω‘≤»Π ΙΟΩΗωakΘ®1ΓήkΓήmΘ§kΓ NΘ©ΕΦ «ΤδΉσ”“œύΝΎΝΫΗω ΐΤΫΖΫΒΡΒ»±»÷–œνΘ§‘ρ’ΐ’ϊ ΐmΒΡΉν–Γ÷Β « Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΒΞΈΜ”–‘±ΙΛ1000ΟϊΘ§ΤΫΨυΟΩ»ΥΟΩΡξ¥¥‘λάϊ»σ10Άρ‘ΣΘ°ΈΣΝΥ‘ωΦ”Τσ“ΒΨΚ’υΝΠΘ§ΨωΕ®”≈Μ·≤ζ“ΒΫαΙΙΘ§Βς’ϊ≥ωxΘ®xΓ N*Θ©Οϊ‘±ΙΛ¥” ¬ΒΎ»ΐ≤ζ“ΒΘ§Βς’ϊΚσΥϊΟ«ΤΫΨυΟΩ»ΥΟΩΡξ¥¥‘λάϊ»σΈΣ10Θ®a©¹ ![]() Θ©Άρ‘ΣΘ®aΘΨ0Θ©Θ§ Θœ¬ΒΡ‘±ΙΛΤΫΨυΟΩ»ΥΟΩΡξ¥¥‘λΒΡάϊ»σΈΣ‘≠ά¥Θ®1+
Θ©Άρ‘ΣΘ®aΘΨ0Θ©Θ§ Θœ¬ΒΡ‘±ΙΛΤΫΨυΟΩ»ΥΟΩΡξ¥¥‘λΒΡάϊ»σΈΣ‘≠ά¥Θ®1+ ![]() Θ©±ΕΘ°
Θ©±ΕΘ°
Θ®1Θ©»τ“Σ±Θ÷Λ Θ”ύ‘±ΙΛ¥¥‘λΒΡΡξΉήάϊ»σ≤ΜΒΆ”Ύ‘≠ά¥1000Οϊ‘±ΙΛ¥¥‘λΒΡΡξΉήάϊ»σΘ§‘ρΉνΕύΩ…“‘’ϊ≥ωΕύ…ΌΟϊ‘±ΙΛ¥” ¬ΒΎ»ΐ≤ζ“ΒΘΜ
Θ®2Θ©»τΒς’ϊ≥ωΒΡ‘±ΙΛ¥¥‘λΒΡΡξΉήάϊ»σ Φ÷’≤ΜΗΏ”Ύ Θ”ύ‘±ΙΛ¥¥‘λΒΡΡξΉήάϊ»σΘ§‘ρaΒΡΉν¥σ»Γ÷Β «Εύ…ΌΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
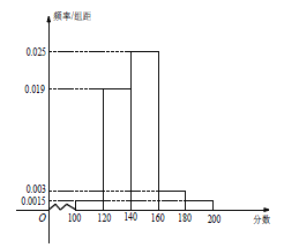
ΓΨΧβΡΩΓΩΦΉ““ΝΫΗωΆ§―ßΫχ––Ε®ΒψΆΕάΚ”ΈœΖΘ§“―÷ΣΥϊΟ«ΟΩ“Μ¥ΈΆΕάΚΆΕ÷–ΒΡΗ≈¬ ΨυΈΣ![]() Θ§«“Ης¥ΈΆΕάΚΒΡΫαΙϊΜΞ≤Μ”ΑœλΘ°ΦΉΆ§―ßΨωΕ®ΆΕ5¥ΈΘ§““Ά§―ßΨωΕ®ΆΕ÷–1¥ΈΨΆΆΘ÷ΙΘ§Ζώ‘ρΨΆΦΧ–χΆΕœ¬»ΞΘ§ΒΪΆΕάΚ¥Έ ΐ≤Μ≥§Ιΐ5¥ΈΘ°
Θ§«“Ης¥ΈΆΕάΚΒΡΫαΙϊΜΞ≤Μ”ΑœλΘ°ΦΉΆ§―ßΨωΕ®ΆΕ5¥ΈΘ§““Ά§―ßΨωΕ®ΆΕ÷–1¥ΈΨΆΆΘ÷ΙΘ§Ζώ‘ρΨΆΦΧ–χΆΕœ¬»ΞΘ§ΒΪΆΕάΚ¥Έ ΐ≤Μ≥§Ιΐ5¥ΈΘ°
Θ®1Θ©«σΦΉΆ§―ß÷Ν…Ό”–4¥ΈΆΕ÷–ΒΡΗ≈¬ ΘΜ
Θ®2Θ©«σ““Ά§―ßΆΕάΚ¥Έ ΐ![]() ΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊΘ°
ΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥–ΘΈΣ―ΓΑΈ≤ΈΦ”ΓΑ―κ ”≤¬ΒΤΟ’¥σ»ϋΓ±ΒΡΕ”‘±Θ§‘Ύ–ΘΡΎΉι÷·≤¬ΒΤΟ’ΨΚ»ϋ.ΙφΕ®ΘΚΒΎ“ΜΫΉΕΈ÷Σ Ε≤β ‘≥…Φ®≤Μ–Γ”Ύ![]() Ζ÷ΒΡ―ß…ζΫχ»κΒΎΕΰΫΉΕΈ±»»ϋ.œ÷”–
Ζ÷ΒΡ―ß…ζΫχ»κΒΎΕΰΫΉΕΈ±»»ϋ.œ÷”–![]() Οϊ―ß…ζ≤ΈΦ”÷Σ Ε≤β ‘Θ§≤ΔΫΪΥυ”–≤β ‘≥…Φ®Μφ÷Τ≥…»γœ¬Υυ ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ.
Οϊ―ß…ζ≤ΈΦ”÷Σ Ε≤β ‘Θ§≤ΔΫΪΥυ”–≤β ‘≥…Φ®Μφ÷Τ≥…»γœ¬Υυ ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ.
Θ®1Θ©ΙάΥψ’β![]() Οϊ―ß…ζ≤β ‘≥…Φ®ΒΡ÷–ΈΜ ΐΘ§≤Δ«σΫχ»κΒΎΕΰΫΉΕΈ±»»ϋΒΡ―ß…ζ»Υ ΐΘΜ
Οϊ―ß…ζ≤β ‘≥…Φ®ΒΡ÷–ΈΜ ΐΘ§≤Δ«σΫχ»κΒΎΕΰΫΉΕΈ±»»ϋΒΡ―ß…ζ»Υ ΐΘΜ
Θ®2Θ©ΫΪΫχ»κΒΎΕΰΫΉΕΈΒΡ―ß…ζΖ÷≥…»τΗ…Ε”Ϋχ––±»»ϋ.œ÷ΦΉΓΔ““ΝΫΕ”‘Ύ±»»ϋ÷–Ψυ“―ΜώΒΟ![]() Ζ÷Θ§Ϋχ»κΉνΚσ«Ω¥πΫΉΕΈ.«ά¥πΙφ‘ρΘΚ«άΒΫΒΡΕ”ΟΩ¥Έ–η≤¬
Ζ÷Θ§Ϋχ»κΉνΚσ«Ω¥πΫΉΕΈ.«ά¥πΙφ‘ρΘΚ«άΒΫΒΡΕ”ΟΩ¥Έ–η≤¬![]() ΧθΟ’”οΘ§≤¬Ε‘
ΧθΟ’”οΘ§≤¬Ε‘![]() ΧθΒΟ
ΧθΒΟ![]() Ζ÷Θ§≤¬¥μ
Ζ÷Θ§≤¬¥μ![]() ΧθΩέ
ΧθΩέ![]() Ζ÷.ΗυΨίΨ≠―ιΘ§ΦΉΕ”≤¬Ε‘ΟΩΧθΟ’”οΒΡΗ≈¬ ΨυΈΣ
Ζ÷.ΗυΨίΨ≠―ιΘ§ΦΉΕ”≤¬Ε‘ΟΩΧθΟ’”οΒΡΗ≈¬ ΨυΈΣ![]() Θ§““Ε”≤¬Ε‘ΟΩΧθΟ’”οΒΡΗ≈¬ ΨυΈΣ
Θ§““Ε”≤¬Ε‘ΟΩΧθΟ’”οΒΡΗ≈¬ ΨυΈΣ![]() Θ§≤¬Ε‘ΒΎ
Θ§≤¬Ε‘ΒΎ![]() ΧθΒΡΗ≈¬ ΨυΈΣ
ΧθΒΡΗ≈¬ ΨυΈΣ![]() .»τ’βΝΫΧθ«άΒΫ¥πΧβΒΡΜζΜαΨυΒ»Θ§ΡζΉωΈΣ≥ΓΆβΙέ÷Ύœκ÷ß≥÷’βΝΫΕ”÷–ΒΡ”≈ ΛΕ”Θ§ΜαΑ―÷ß≥÷Τ±ΆΕΗχΡΡΕ”ΘΩ
.»τ’βΝΫΧθ«άΒΫ¥πΧβΒΡΜζΜαΨυΒ»Θ§ΡζΉωΈΣ≥ΓΆβΙέ÷Ύœκ÷ß≥÷’βΝΫΕ”÷–ΒΡ”≈ ΛΕ”Θ§ΜαΑ―÷ß≥÷Τ±ΆΕΗχΡΡΕ”ΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ―Γ–ό4ΓΣ4ΘΚΉχ±ξœΒ”κ≤Έ ΐΖΫ≥Χ
‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–«ζœΏ
÷–«ζœΏ![]() Ψ≠…λΥθ±δΜΜ
Ψ≠…λΥθ±δΜΜ![]() ΚσΒΟΒΫ«ζœΏ
ΚσΒΟΒΫ«ζœΏ![]() Θ§‘Ύ“‘
Θ§‘Ύ“‘![]() ΈΣΦΪΒψΘ§
ΈΣΦΪΒψΘ§ ![]() ÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΒΡΦΪΉχ±ξœΒ÷–Θ§«ζœΏ
÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΒΡΦΪΉχ±ξœΒ÷–Θ§«ζœΏ![]() ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ
ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ![]() .
.
Θ®1Θ©«σ«ζœΏ![]() ΒΡ≤Έ ΐΖΫ≥ΧΚΆ
ΒΡ≤Έ ΐΖΫ≥ΧΚΆ![]() ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘΜ
ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘΜ
Θ®2Θ©…η![]() ΈΣ«ζœΏ
ΈΣ«ζœΏ![]() …œΒΡ“ΜΒψΘ§”÷
…œΒΡ“ΜΒψΘ§”÷![]() œρ«ζœΏ
œρ«ζœΏ![]() “ΐ«–œΏΘ§«–ΒψΈΣ
“ΐ«–œΏΘ§«–ΒψΈΣ![]() Θ§«σ
Θ§«σ![]() ΒΡΉν¥σ÷Β.
ΒΡΉν¥σ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®ΈΡΩΤΘ©“―÷ΣΒΡΆ÷‘≤![]() ΒΡΉσΓΔ”“ΝΫΗωΫΙΒψΖ÷±πΈΣ
ΒΡΉσΓΔ”“ΝΫΗωΫΙΒψΖ÷±πΈΣ![]() Θ§…œΕΞΒψ
Θ§…œΕΞΒψ![]() Θ§
Θ§ ![]() «’ΐ»ΐΫ«–Έ«“÷ή≥ΛΈΣ6.
«’ΐ»ΐΫ«–Έ«“÷ή≥ΛΈΣ6.
(1)«σΆ÷‘≤![]() ΒΡ±ξΉΦΖΫ≥ΧΦΑάκ–Ρ¬ ΘΜ
ΒΡ±ξΉΦΖΫ≥ΧΦΑάκ–Ρ¬ ΘΜ
(2) ![]() ΈΣΉχ±ξ‘≠ΒψΘ§
ΈΣΉχ±ξ‘≠ΒψΘ§ ![]() «÷±œΏ
«÷±œΏ![]() …œΒΡ“ΜΗωΕ·ΒψΘ§«σ
…œΒΡ“ΜΗωΕ·ΒψΘ§«σ![]() ΒΡΉν–Γ÷ΒΘ§≤Δ«σ≥ω¥Υ ±Βψ
ΒΡΉν–Γ÷ΒΘ§≤Δ«σ≥ω¥Υ ±Βψ![]() ΒΡΉχ±ξ.
ΒΡΉχ±ξ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com