
【题目】袋子里有完全相同的3只红球和4只黑球,今从袋子里随机取球.
(Ⅰ)若有放回地取3次,每次取一个球,求取出2个红球1个黑球的概率;
(Ⅱ)若无放回地取3次,每次取一个球,若取出每只红球得2分,取出每只黑球得1分,求得分![]() 的分布列和数学期望.
的分布列和数学期望.
 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】对于函数f(x)定义域中任意的x1 , x2(x1≠x2),有如下结论:
(1)f(x1+x2)=f(x1)f(x2)
(2)f(x1x2)=f(x1)+f(x2)
(3) ![]()
当f(x)=ex时,上述结论中正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P是圆x2+y2=4上一动点,PD⊥x轴于点D,记满足 ![]() =
= ![]() (
( ![]() +
+ ![]() )的动点M的轨迹为Γ. (Ⅰ)求轨迹Γ的方程;
)的动点M的轨迹为Γ. (Ⅰ)求轨迹Γ的方程;
(Ⅱ)已知直线l:y=kx+m与轨迹F交于不同两点A,B,点G是线段AB中点,射线OG交轨迹Γ于点Q,且 ![]() =λ
=λ ![]() ,λ∈R.
,λ∈R.
①证明:λ2m2=4k2+1;
②求△AOB的面积S(λ)的解析式,并计算S(λ)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知acosB+bcosA=2ccosC.
(1)求角C的大小;
(2)若a=5,b=8,求边c的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=a(x-lnx)+![]() ,a∈R.
,a∈R.
(I)讨论f(x)的单调性;
(II)当a=1时,证明f(x)>f’(x)+![]() 对于任意的x∈[1,2] 恒成立。
对于任意的x∈[1,2] 恒成立。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 与
与![]() 的中心在原点,焦点分别在
的中心在原点,焦点分别在![]() 轴与
轴与![]() 轴上,它们有相同的离心率
轴上,它们有相同的离心率![]() ,并且
,并且![]() 的短轴为
的短轴为![]() 的长轴,
的长轴,![]() 与
与![]() 的四个焦点构成的四边形面积是
的四个焦点构成的四边形面积是![]() .
.
(1)求椭圆![]() 与
与![]() 的方程;
的方程;
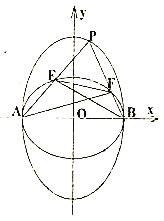
(2)设![]() 是椭圆
是椭圆![]() 上非顶点的动点,
上非顶点的动点,![]() 与椭圆
与椭圆![]() 长轴两个顶点
长轴两个顶点![]() ,
,![]() 的连线
的连线![]() ,
,![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() ,
,![]() 点.
点.
(i)求证:直线![]() ,
,![]() 斜率之积为常数;
斜率之积为常数;
(ii)直线![]() 与直线
与直线![]() 的斜率之积是否为常数?若是,求出该值;若不是,说明理由.
的斜率之积是否为常数?若是,求出该值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+bx2+2x在x=﹣1处取得极值,且在点(1,f(1))处的切线的斜率为2. (Ⅰ)求a,b的值:
(Ⅱ)若关于x的方程f(x)+x3﹣2x2﹣x+m=0在[ ![]() ,2]上恰有两个不相等的实数根,求实数m的取值范围.
,2]上恰有两个不相等的实数根,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com