
 =(cos23°,cos67°),
=(cos23°,cos67°), =(2cos68°,2cos22°),则△ABC的面积为________.
=(2cos68°,2cos22°),则△ABC的面积为________.
 、
、 的坐标,可得
的坐标,可得 、
、 的模,由数量积公式,可得
的模,由数量积公式,可得 •
• 的值,进而由cos∠B=
的值,进而由cos∠B=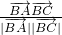 ,可得cos∠B,由余弦函数的性质,可得∠B,最后由三角形面积公式,计算可得答案.
,可得cos∠B,由余弦函数的性质,可得∠B,最后由三角形面积公式,计算可得答案. =(cos23°,cos67°),则
=(cos23°,cos67°),则 =-(cos23°,sin23°),有|
=-(cos23°,sin23°),有| |=1,
|=1, =(2cos68°,2cos22°)=2(cos68°,sin68°),则|
=(2cos68°,2cos22°)=2(cos68°,sin68°),则| |=2,
|=2, •
• =-2(cos23°cos68°-sin23°sin68°)=-2×cos45°=-
=-2(cos23°cos68°-sin23°sin68°)=-2×cos45°=- ,
,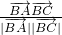 =-
=- ,
, |
| |•|
|•| |sin∠B=
|sin∠B= ×1×2×
×1×2× =
= ;
; .
. •
• ,注意角B是向量
,注意角B是向量 、
、 的夹角.
的夹角. 

科目:高中数学 来源: 题型:
| a |
| 2 |
| 3 |
| 2 |
| 3 |
| OA |
| a |
| b |
| OB |
| a |
| b |
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南师大附中海口中学高三第五次月考数学试卷(文科)(解析版) 题型:选择题
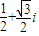
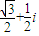
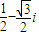
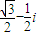
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com