
分析 (1)运用题设和实际建立函数关系并确定定义域;
(2)运用基本不等式求函数的最值和取得最值的条件.
解答 解:(1)由题意,F=15×$\frac{120}{x+5}$+0.5x=$\frac{1800}{x+5}$+0.5x(x≥0).
(2)因为$\frac{1800}{x+5}$+0.5x=$\frac{1800}{x+5}$+0.5(x+5)-2.5≥2$\sqrt{1800×0.5}$-2.5=57.5,
当且仅当$\frac{1800}{x+5}$=0.5(x+5),即x=55时取等号.
所以当x为55平方米时,F取得最小值为57.5万元.
点评 本题考查函数最值的应用,着重考查阅读理解能力和数学建模能力、基本不等式及在解决实际问题中的灵活运用.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -7 | B. | -14 | C. | 7 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<0} | B. | {x|0<x<4} | C. | {x|x≥4} | D. | R |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4031 | B. | -4032 | C. | -4033 | D. | -4034 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
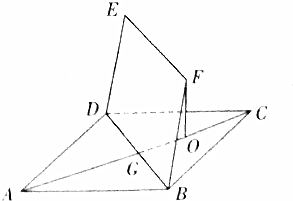 如图,正方形ABCD的边长为2$\sqrt{2}$,四边形BDEF是平行四边形,BD与AC交于点G,O为GC的中点,且FO⊥平面ABCD,FO=$\sqrt{3}$.
如图,正方形ABCD的边长为2$\sqrt{2}$,四边形BDEF是平行四边形,BD与AC交于点G,O为GC的中点,且FO⊥平面ABCD,FO=$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com