
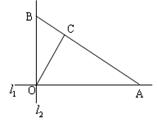
(本题16分)如图,在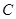 城周边已有两条公路
城周边已有两条公路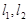 在点O处交汇,且它们的夹角为
在点O处交汇,且它们的夹角为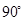 .已知
.已知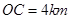 ,
, 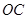 与公路
与公路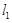 夹角为
夹角为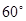 .现规划在公路
.现规划在公路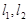 上分别选择
上分别选择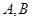 两处作为交汇点(异于点O)直接修建一条公路通过
两处作为交汇点(异于点O)直接修建一条公路通过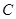 城.设
城.设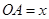
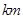 ,
,
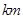 .
.
(1) 求出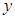 关于
关于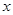 的函数关系式并指出它的定义域;
的函数关系式并指出它的定义域;
(2) 试确定点A,B的位置,使△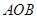 的面积最小.
的面积最小.
科目:高中数学 来源: 题型:
(本题16分)
如图,F是抛物线![]() 的焦点,Q是准线与
的焦点,Q是准线与![]() 轴的交点,斜率为
轴的交点,斜率为![]() 的直线
的直线![]() 经过点Q.
经过点Q.
(1)当K取不同数值时,求直线![]() 与抛物线交点的个数;
与抛物线交点的个数;
(2)如直线![]() 与抛物线相交于A、B两点,求证:
与抛物线相交于A、B两点,求证:![]() 是定值
是定值
(3)在![]() 轴上是否存在这样的定点M,对任意的过点Q的直线
轴上是否存在这样的定点M,对任意的过点Q的直线![]() ,如
,如![]() 与抛物线相交于A、B两点,均能使得
与抛物线相交于A、B两点,均能使得![]() 为定值,有则找出满足条
为定值,有则找出满足条
件的点M;没有,则说明理由.
查看答案和解析>>
科目:高中数学 来源:2010届上海市虹口区高三第二次模拟考试数学卷 题型:解答题
(本题16分)
如图所示,某人在斜坡P处仰视正对 面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为
面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为 ,
,
(1)以射线OC为 轴的正向,OB为
轴的正向,OB为 轴正向,建立直角坐标系,求
轴正向,建立直角坐标系,求 出斜坡CD所在直线方程;
出斜坡CD所在直线方程;
(2)当观察者P视角∠APB最大时,求点P的坐标(人的身高忽略不计).
查看答案和解析>>
科目:高中数学 来源:江苏省09-10学年度第一学期第三次月考高一数学 题型:解答题
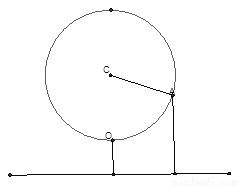
(本题16分)如图,某大风车的半径为2米,每12秒沿逆时针方向旋转一周,它的最底点 离地面1米,风车圆周上一点A从最底点
离地面1米,风车圆周上一点A从最底点 开始,运动t秒后与地面距离为h米,
开始,运动t秒后与地面距离为h米,
(1)求函数h=f(t)的关系式, 并在给出的方格纸上用五点作图法作出h=f(t)在一个周期内的图象(要列表,描点);
(2) A从最底点 开始, 沿逆时针方向旋转第一周内,有多长时间离地面的高度超过4米?
开始, 沿逆时针方向旋转第一周内,有多长时间离地面的高度超过4米?

查看答案和解析>>
科目:高中数学 来源:2010届上海市虹口区高三第二次模拟考试数学卷 题型:解答题
(本题16分)
如图,F是抛物线 的焦点,Q是准线与
的焦点,Q是准线与 轴的交点,斜率为
轴的交点,斜率为 的直线
的直线 经过点Q.
经过点Q.
(1)当K取不同数值时,求直线 与抛物线交点的个数;
与抛物线交点的个数;
(2)如直线 与抛物线相交于A、B两点,求证:
与抛物线相交于A、B两点,求证: 是定值
是定值
(3)在 轴上是否存在这样的定点M,对任意的过点Q的直线
轴上是否存在这样的定点M,对任意的过点Q的直线 ,如
,如 与抛物线相交于A、B两点,均能使得
与抛物线相交于A、B两点,均能使得 为定值,有则找出满足条
为定值,有则找出满足条
件的点M;没有,则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com