
【题目】如图,四边形![]() 为矩形,
为矩形,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上的动点.
上的动点.
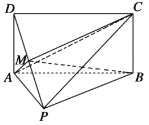
(1)若![]() 为线段
为线段![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)若三棱锥![]() 的体积记为
的体积记为![]() ,四棱锥
,四棱锥![]() 的体积记为
的体积记为![]() ,当
,当![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)连接![]() ,
,![]() ,记它们的交点为
,记它们的交点为![]() ,连接
,连接![]() ,利用中位线可得
,利用中位线可得![]() ,再利用线面平行的判定定理可证.
,再利用线面平行的判定定理可证.
(2)设![]() ,取
,取![]() 中点
中点![]() ,利用三棱锥的体积公式和
,利用三棱锥的体积公式和![]() ,可得
,可得![]() ,再建立空间直角坐标系,利用向量可得二面角
,再建立空间直角坐标系,利用向量可得二面角![]() 的余弦值.
的余弦值.
(1)连接![]() ,
,![]() ,记它们的交点为
,记它们的交点为![]() ,连接
,连接![]()
因为四边形![]() 为矩形,∴
为矩形,∴![]() 为
为![]() 中点,
中点,
又![]() 为线段
为线段![]() 的中点,∴
的中点,∴![]() ,
,
而![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]() .
.
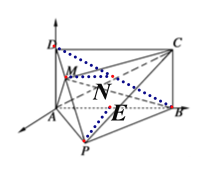
(2)∵矩形![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,
,
设![]() ,取
,取![]() 中点
中点![]() ,
,
因为![]() 是等边三角形,∴
是等边三角形,∴![]() ,
,
又因为![]() 平面
平面![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,且
,且![]() ,
,
设三棱锥![]() 的高为
的高为![]() ,则
,则![]() ,∴
,∴![]() ,
,
由![]() 得
得![]() ,解得
,解得![]() ,
,
由题意,如图以![]() 点为坐标原点建立空间直角坐标系,则
点为坐标原点建立空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]()
∵![]() ,∴
,∴![]() ,
,
易知平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则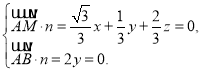
令![]() 则得平面
则得平面![]() 的一个法向量
的一个法向量![]() ,
,
![]()
因为二面角![]() 为锐角二面角,
为锐角二面角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为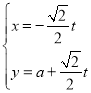 (t为参数,a∈R),以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ
(t为参数,a∈R),以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ
(1)求直线l的普通方程及曲线C的直角坐标方程;
(2)若直线l过点P(1,1)且与曲线C交于AB两点,求|PA|+|PB|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直角梯形ABCD如图(1)所示,其中![]() ,
,![]() ,过点B作
,过点B作![]() ,垂足为M,得到面积为4的正方形ABMD,现沿BM进行翻折,得到如图(2)所示的四棱柱C-ABMD.
,垂足为M,得到面积为4的正方形ABMD,现沿BM进行翻折,得到如图(2)所示的四棱柱C-ABMD.
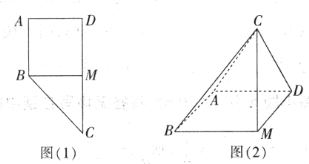
(1)求证:平面![]() 平面CDM;
平面CDM;
(2)若![]() ,平面CBM与平面CAD所成锐二面角的余弦值为
,平面CBM与平面CAD所成锐二面角的余弦值为![]() ,求CM的长.
,求CM的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高铁是我国国家名片之一,高铁的修建凝聚着中国人的智慧与汗水.如图所示,B、E、F为山脚两侧共线的三点,在山顶A处测得这三点的俯角分别为![]() 、
、![]() 、
、![]() ,计划沿直线BF开通穿山隧道,现已测得BC、DE、EF三段线段的长度分别为3、1、2.
,计划沿直线BF开通穿山隧道,现已测得BC、DE、EF三段线段的长度分别为3、1、2.
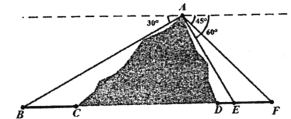
(1)求出线段AE的长度;
(2)求出隧道CD的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到点
到点![]() 的距离与它到直线
的距离与它到直线![]() 的距离
的距离![]() 的比值为
的比值为![]() ,设动点
,设动点![]() 形成的轨迹为曲线
形成的轨迹为曲线![]() ..
..
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 两点,过
两点,过![]() 点作
点作![]() ,垂足为
,垂足为![]() ,过
,过![]() 点作
点作![]() ,垂足为
,垂足为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com