解:(1)连接DM
∵DE是半圆C的直径,∴∠DME=90°
∵FE:FD=4:3,∴可设FE=4x,则FD=3x,∴DE=5x

∵AD平分∠BAC,∴∠BAD=∠DAC
∵∠B=∠CAE
∴∠BAD+∠B=∠DAC+∠CAE
∵∠ADE=∠BAD+∠B
∴∠ADE=∠DAE
∴EA=ED
∵DE是半圆C的直径
∴∠DFE=90°
∴AF=DF
∴AE=DE=5x,AF=FD=3x
∵AF•AD=AM•AE
∴3x(3x+3x)=AM•5x
∴AM=
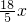
∴ME=AE-AM=5x-
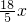
=
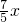
∴cos∠AED=
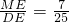
;
(2)过A点作AN⊥BE于N
∵cos∠AED=

,∴sin∠AED=

,∴AN=

AE=
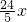
在△CAE和△ABE中
∵∠CAE=∠B,∠AEC=∠BEA
∴△CAE∽△ABE
∴

=
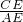
∴AE
2=BE•CE
∴(5x)
2=(10+5x)•

x
∴x=2
∴AN=

又BC=BD+DC=10+5=15
∴S
△ABC=

BC•AN=
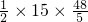
=72.
分析:(1)求∠AED的余弦值,即求ME:DM,由已知条件,勾股定理,切割线定理的推论可以求出;
(2)根据△ABC的面积公式求出BC,AN的长是关键,根据题意由三角函数及相似比即可求出.
点评:本题考查相似三角形的判定,切割线定理,勾股定理,考查三角形面积的计算,属于中档题.

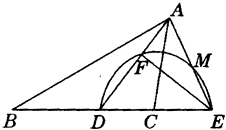 已知在△ABC中,AD为∠BAC的平分线,以C为圆心,CD为半径的半圆交BC的延长线于点E,交AD于点F,交AE于点M,且∠B=∠CAE,EF:FD=4:3.
已知在△ABC中,AD为∠BAC的平分线,以C为圆心,CD为半径的半圆交BC的延长线于点E,交AD于点F,交AE于点M,且∠B=∠CAE,EF:FD=4:3.
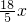
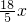 =
=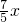
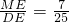 ;
; ,∴sin∠AED=
,∴sin∠AED= ,∴AN=
,∴AN= AE=
AE=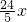
 =
=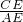
 x
x
 BC•AN=
BC•AN=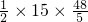 =72.
=72.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案