
分析 根据特殊角的三角函数值及x的范围得出x的值.
解答 解:(1)∵cos$\frac{π}{6}$=$\frac{\sqrt{3}}{2}$,∴x=$\frac{π}{6}$.
(2)∵cos$\frac{2π}{3}$=-$\frac{1}{2}$,∴x=$\frac{2π}{3}$.
(3)∵cos$\frac{π}{4}$=cos$\frac{7π}{4}$=$\frac{\sqrt{2}}{2}$,∴x=$\frac{π}{4}$或x=$\frac{7π}{4}$.
(4)∵cos$\frac{5π}{6}$=cos(-$\frac{5π}{6}$)=-$\frac{\sqrt{3}}{2}$.∴x=$\frac{5π}{6}$或x=-$\frac{5π}{6}$.
点评 本题考查了特殊角的三角函数,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题“若|x|=1,则x=1”的否命题为:“若|x|=1,则x≠1” | |
| B. | “x=3”是“”“x2=9”的必要不充分条件 | |
| C. | 命题“存在x∈R,使得x2+x+1≤0”的否定是:对任意x∈R,均有x2+x+1>0” | |
| D. | 命题“若x=y,则sinx=siny”的逆命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
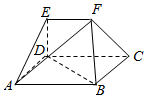 如图,在多面体ABCDEF中,四边形ABCD为矩形,△ADE,△BCF均为等边三角形,EF∥AB,EF=AD=$\frac{1}{2}$AB.
如图,在多面体ABCDEF中,四边形ABCD为矩形,△ADE,△BCF均为等边三角形,EF∥AB,EF=AD=$\frac{1}{2}$AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com