
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系xoy中,直线l的参数方程为 ![]() (t为参数,
(t为参数, ![]() ),以坐标原点o为极点,x轴的正半轴为极轴,并取相同的长度单位,建立极坐标系.曲线
),以坐标原点o为极点,x轴的正半轴为极轴,并取相同的长度单位,建立极坐标系.曲线 ![]()
(1)若直线l曲线 ![]() 相交于点
相交于点 ![]() ,
, ![]() ,
, ![]() ,证明:
,证明: ![]() 为定值;
为定值;
(2)将曲线 ![]() 上的任意点
上的任意点 ![]() 作伸缩变换
作伸缩变换 ![]() 后,得到曲线
后,得到曲线 ![]() 上的点
上的点 ![]() ,求曲线
,求曲线 ![]() 的内接矩形
的内接矩形 ![]() 周长的最大值.
周长的最大值.
科目:高中数学 来源: 题型:
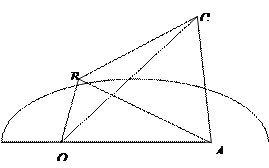
【题目】如图,半圆![]() 的直径为
的直径为![]() ,
, ![]() 为直径延长线上的一点,
为直径延长线上的一点, ![]() ,
, ![]() 为半圆上任意一点,以
为半圆上任意一点,以![]() 为一边作等边三角形
为一边作等边三角形![]() ,设
,设![]()
![]() .
.
(1)当![]() 为何值时,四边形
为何值时,四边形![]() 面积最大,最大值为多少;
面积最大,最大值为多少;
(2)当![]() 为何值时,
为何值时, ![]() 长最大,最大值为多少.
长最大,最大值为多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
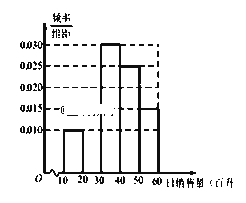
【题目】某加油站20名员工日销售量的频率分布直方图,如图所示:
(1)补全该频率分布直方图在[20,30)的部分,并分别计算日销售量在 [10,20),[20,30)的员工数;
(2)在日销量为[10,30)的员工中随机抽取2人,求这两名员工日销量在 [20,30)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是____________.
【答案】![]()
【解析】∵圆C的方程可化为(x-4)2+y2=1,∴圆C的圆心为(4,0),半径为1.由题意知,直线y=kx-2上至少存在一点A(x0,kx0-2),以该点为圆心,1为半径的圆与圆C有公共点,∴存在x0∈R,使得AC≤1+1成立,即ACmin≤2.
∵ACmin即为点C到直线y=kx-2的距离![]() ,
,
∴![]() ≤2,解得0≤k≤
≤2,解得0≤k≤![]() .∴k的最大值是
.∴k的最大值是![]() .
.
【题型】填空题
【结束】
15
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() .
.
(1)若直线![]() 与直线
与直线![]() 平行,求实数
平行,求实数![]() 的值;
的值;
(2)若![]() ,
, ![]() ,点
,点![]() 在直线
在直线![]() 上,已知
上,已知![]() 的中点在
的中点在![]() 轴上,求点
轴上,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举办校园科技文化艺术节,在同一时间安排《生活趣味数学》和《校园舞蹈赏析》两场讲座.已知A、B两学习小组各有5位同学,每位同学在两场讲座任意选听一场.若A组1人选听《生活趣味数学》,其余4人选听《校园舞蹈赏析》;B组2人选听《生活趣味数学》,其余3人选听《校园舞蹈赏析》.
(1)若从此10人中任意选出3人,求选出的3人中恰有2人选听《校园舞蹈赏析》的概率;
(2)若从A、B两组中各任选2人,设X为选出的4人中选听《生活趣味数学》的人数,求X的分布列和数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量m ![]() (sin
(sin ![]() ,1),
,1), ![]() =(1,
=(1, ![]() cos
cos ![]() ),函数f(x)=
),函数f(x)= ![]()
(1)求函数f(x)的最小正周期;
(2)若f(α﹣ ![]() )=
)= ![]() ,求f(2α+
,求f(2α+ ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究函数f(x)= ![]() 的性质,完成下面两个问题:
的性质,完成下面两个问题:
①将f(2),f(3),f(5)按从小到大排列为;
②函数g(x)= ![]() (x> 0)的最大值为 .
(x> 0)的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂拟建一个下部为圆柱,上部为半球的容器(如图圆柱高为 ![]() ,半径为
,半径为 ![]() ,不计厚度,单位:米),按计划容积为
,不计厚度,单位:米),按计划容积为 ![]() 立方米,且
立方米,且 ![]() ,假设建造费用仅与表面积有关(圆柱底部不计 ),已知圆柱部分每平方米的费用为2千元,半球部分每平方米的费用为2千元,设该容器的建造费用为y千元.
,假设建造费用仅与表面积有关(圆柱底部不计 ),已知圆柱部分每平方米的费用为2千元,半球部分每平方米的费用为2千元,设该容器的建造费用为y千元.
(1)求y关于r的函数关系,并求其定义域;
(2)求建造费用最小时的 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com