
【题目】已知三棱柱![]() 内接于一个半径为
内接于一个半径为![]() 的球,四边形
的球,四边形![]() 与
与![]() 均为正方形,
均为正方形,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角的余弦值为( )
所成角的余弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
画出图形,找出BM与AN所成角的平面角,利用解三角形求出BM与AN所成角的余弦值.
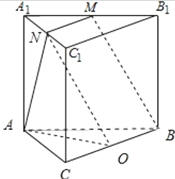
直三棱柱ABCA1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,
如图:BC的中点为O,连结ON,
MN∥![]() B1C1=OB,则MNOB是平行四边形,BM与AN所成角就是∠ANO,
B1C1=OB,则MNOB是平行四边形,BM与AN所成角就是∠ANO,
∵![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() ,
,
可得A1C1⊥B1C1,
四边形![]() 与
与![]() 均为正方形,可得BC=CA=CC1,
均为正方形,可得BC=CA=CC1,
∵三棱柱![]() 内接于一个半径为
内接于一个半径为![]() 的球,
的球,
设BC=CA=CC1=a,
三棱柱![]() 外接球可看作棱长为a的正方体外接球,
外接球可看作棱长为a的正方体外接球,
∴![]() ,解得a=2,
,解得a=2,
∴BC=CA=CC1=2,
CO=1,AO=![]() ,AN=
,AN=![]() ,
,![]() ,
,
在△ANO中,由余弦定理可得:
![]() ,
,
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
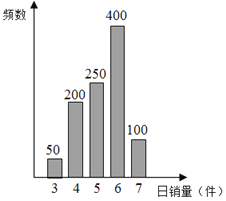
【题目】某公司销售部随机抽取了1000名销售员1天的销售记录,经统计,其柱状图如图.
该公司给出了两种日薪方案.
方案1:没有底薪,每销售一件薪资20元;
方案2:底薪90元,每日前5件的销售量没有奖励,超过5件的部分每件奖励20元.
(1)分别求出两种日薪方案中日工资y(单位:元)与销售件数n的函数关系式;
(2)若将频率视为概率,回答下列问题:
(Ⅰ)根据柱状图,试分别估计两种方案的日薪X(单位:元)的数学期望及方差;
(Ⅱ)如果你要应聘该公司的销售员,结合(Ⅰ)中的数据,根据统计学的思想,分析选择哪种薪资方案比较合适,并说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PPD//平面MAC,PA=PD=![]() ,AB=4.
,AB=4.
(I)求证:M为PB的中点;
(II)求二面角B-PD-A的大小;
(III)求直线MC与平面BDP所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
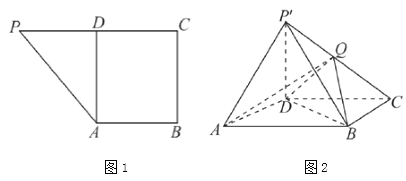
【题目】如图1所示,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 恰好在线段
恰好在线段![]() 的垂直平分线上,以
的垂直平分线上,以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且平面
的位置,且平面![]() 底面
底面![]() ,如图2所示,
,如图2所示,![]() 是线段
是线段![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)若三棱锥![]() 的体积为1,求
的体积为1,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 与直四棱柱
与直四棱柱![]() 组合而成的几何体中,四边形
组合而成的几何体中,四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() 平面
平面![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)证明:![]() 平面
平面![]() ;
;
(2)动点![]() 在线段
在线段![]() 上(包括端点),若二面角
上(包括端点),若二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解高三学生的“理科综合”成绩是否与性别有关,某校课外学习兴趣小组在本地区高三年级理科班中随机抽取男、女学生各100名,然后对这200名学生在一次联合模拟考试中的“理科综合”成绩进行统计规定:分数不小于240分为“优秀”小于240分为“非优秀”.
(1)根据题意,填写下面的2×2列联表,并根据列联表判断是否有90%以上的把握认为“理科综合”成绩是否优秀与性别有关.
性别 | 优秀 | 非优秀 | 总计 |
男生 | 35 | ||
女生 | 75 | ||
总计 |
(2)用分层抽样的方法从成绩优秀的学生中随机抽取12名学生,然后再从这12名学生中抽取3名参加某高校举办的自主招生考试,设抽到的3名学生中女生的人数为X,求X的分布列及数学期望.
附: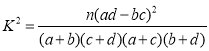 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com