
【题目】如图1所示,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 恰好在线段
恰好在线段![]() 的垂直平分线上,以
的垂直平分线上,以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且平面
的位置,且平面![]() 底面
底面![]() ,如图2所示,
,如图2所示,![]() 是线段
是线段![]() 的中点.
的中点.
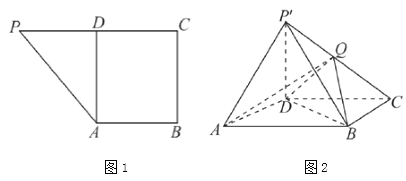
(1)证明:![]() 平面
平面![]() ;
;
(2)若三棱锥![]() 的体积为1,求
的体积为1,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)3.
【解析】
(1)由直角梯形中各线段关系,得到![]() ,结合平面
,结合平面![]() 底面
底面![]() ,可得
,可得![]() ,结合
,结合![]() ,得到
,得到![]() 平面
平面![]() ,从而有
,从而有![]() ,通过三线合一得到
,通过三线合一得到![]() ,即可证明
,即可证明![]() 平面
平面![]() ;
;
(2)利用(1)中结论及已知条件,证明![]() 平面
平面![]() ,利用
,利用![]() 表示出三棱锥
表示出三棱锥![]() 的体积,列方程解出
的体积,列方程解出![]() 的值即可.
的值即可.
(1)在直角梯形![]() 中,
中,
![]() 点
点![]() 恰好在线段
恰好在线段![]() 的垂直平分线上,
的垂直平分线上,![]() .
.
![]()
![]() 即为线段
即为线段![]() 的垂直平分线,即
的垂直平分线,即![]() 是线段
是线段![]() 的中点,
的中点,
![]()
![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 为矩形,
为矩形,
![]() ,平面
,平面![]() 底面
底面![]() ,
,
平面![]() 底面
底面![]() ,
,
![]()
![]() 底面
底面![]() ,
,
又![]() 底面
底面![]() ,
,
![]()
![]() .
.
又![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
![]()
![]() ,
,
![]() 是线段
是线段![]() 的中点,
的中点,![]() ,
,
![]()
![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
(2)由(1)知,![]() 底面
底面![]() ,
,
又![]() 底面
底面![]()
![]()
![]() ,
,
又![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ,
,
![]()
![]() 是线段
是线段![]() 的中点,
的中点,
![]()
![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
由(1)及![]() ,得
,得![]() ,
,
而![]() ,
,
解得![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】为了研究“教学方式”对教学质量的影响,某高中老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
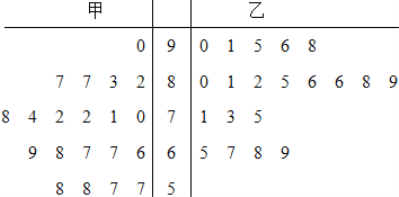
(1)现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;
(2)学校规定:成绩不低于75分的为优秀.请填写下面的2×2列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣1)ex+ax2(a∈R).
(1)若a=e,求函数f(x)在点(1,f(1))处的切线方程;
(2)讨论函数f(x)的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信运动是由腾讯开发的一个类似计步数据库的公众账号,很多手机用户加入微信运动后,为了让自己的步数能领先于朋友,运动的积极性明显增强.微信运动公众号为了解用户的一些情况,在微信运动用户中随机抽取了100名用户,统计了他们某一天的步数,数据整理如下:
|
|
|
|
|
|
|
|
| 5 | 20 | 50 | 18 | 3 | 3 | 1 |
(Ⅰ)根据表中数据,在如图所示的坐标平面中作出其频率分布直方图,并在纵轴上标明各小长方形的高;
(Ⅱ)若视频率分布为概率分布,在微信运动用户中随机抽取3人,求至少2人步数多于1.2万步的概率;
(Ⅲ)若视频率分布为概率分布,在微信运动用户中随机抽取2人,其中每日走路不超过0.8万步的有![]() 人,超过1.2万步的有
人,超过1.2万步的有![]() 人,设
人,设![]() ,求的分布列及数学期望.
,求的分布列及数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 的两交点间距离为
的两交点间距离为![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)如图,设![]() 是椭圆
是椭圆![]() 上的一动点,由原点
上的一动点,由原点![]() 向圆
向圆![]() 引两条切线,分别交椭圆
引两条切线,分别交椭圆![]() 于点
于点![]() ,若直线
,若直线![]() 的斜率均存在,并分别记为
的斜率均存在,并分别记为![]() ,求证:
,求证:![]() 为定值.
为定值.
(3)在(2)的条件下,试问![]() 是否为定值?若是,求出该值;若不是,请说明理由.
是否为定值?若是,求出该值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】坐标系与参数方程:在平面直角坐标系中,以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,已知点
轴的非负半轴为极轴建立极坐标系,已知点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且点
,且点![]() 在直线
在直线![]() 上
上
(Ⅰ)求![]() 的值和直线
的值和直线![]() 的直角坐标方程及
的直角坐标方程及![]() 的参数方程;
的参数方程;
(Ⅱ)已知曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),直线
为参数),直线![]() 与
与![]() 交于
交于![]() 两点,求
两点,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线Γ:y2=2px(p>0)的焦点为F,P是抛物线Γ上一点,且在第一象限,满足![]() (2,2
(2,2![]() )
)
(1)求抛物线Γ的方程;
(2)已知经过点A(3,﹣2)的直线交抛物线Γ于M,N两点,经过定点B(3,﹣6)和M的直线与抛物线Γ交于另一点L,问直线NL是否恒过定点,如果过定点,求出该定点,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,焦距为
,焦距为![]() ,过点
,过点![]() 作直线交椭圆
作直线交椭圆![]() 于
于![]() 两点,
两点,![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若斜率为![]() 的直线
的直线![]() 与椭圆相交于
与椭圆相交于![]() 两点,求定点
两点,求定点![]() 与交点
与交点![]() 所构成的三角形
所构成的三角形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com