
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 的两交点间距离为
的两交点间距离为![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)如图,设![]() 是椭圆
是椭圆![]() 上的一动点,由原点
上的一动点,由原点![]() 向圆
向圆![]() 引两条切线,分别交椭圆
引两条切线,分别交椭圆![]() 于点
于点![]() ,若直线
,若直线![]() 的斜率均存在,并分别记为
的斜率均存在,并分别记为![]() ,求证:
,求证:![]() 为定值.
为定值.
(3)在(2)的条件下,试问![]() 是否为定值?若是,求出该值;若不是,请说明理由.
是否为定值?若是,求出该值;若不是,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 为定值
为定值![]() ;(3)
;(3)![]() 为定值,定值为25.
为定值,定值为25.
【解析】
(1)由椭圆的离心率公式求得![]() ,由椭圆过点
,由椭圆过点![]() ,代入椭圆方程,即可求得
,代入椭圆方程,即可求得![]() 和
和![]() 的值,求得椭圆方程;
的值,求得椭圆方程;
(2)利用点到直线距离公式![]() ,同理求得:
,同理求得:![]() ,则
,则![]() ,
,![]() 是方程
是方程![]() 的两个不相等的实根,根据韦达定理即可求得
的两个不相等的实根,根据韦达定理即可求得![]() 为定值;
为定值;
(3)将直线![]() 和
和![]() 的方程,代入椭圆方程,即可求得
的方程,代入椭圆方程,即可求得![]() 和
和![]() 点坐标,根据两点之间的距离公式
点坐标,根据两点之间的距离公式![]() ,由
,由![]() ,即可求得
,即可求得![]() 为定值.
为定值.
解:(1)由椭圆的离心率![]() ,则
,则![]() ,
,
由直线过点![]() ,代入
,代入![]() ,解得:
,解得:![]() ,则
,则![]() ,
,
![]() 椭圆的标准方程:
椭圆的标准方程:![]() ;
;
(2)证明:由直线![]() ,直线
,直线![]() ,
,
由直线![]() 为圆
为圆![]() 的切线,
的切线,
![]() ,
,![]() ,
,
同理可得:![]() ,
,
![]() ,
,![]() 是方程
是方程![]() 的两个不相等的实根,
的两个不相等的实根,
由![]() ,△
,△![]() ,则
,则![]() ,
,
由![]() ,
,![]() 在椭圆上,即
在椭圆上,即![]() ,
,
 ,
,
![]() 为定值
为定值![]() ;
;
(3)经判断![]() 为定值,
为定值,
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
联立 ,解得
,解得 ,
,
![]() ,
,
同理,得![]() ,
,
由![]() ,
,
得![]() ,
,
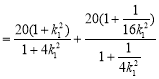 ,
,
 ,
,
![]() ,
,
![]() 为定值,定值为25.
为定值,定值为25.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() ,g(x)
,g(x)![]() 1.
1.
(1)若f(a)=2,求实数a的值;
(2)判断f(x)的单调性,并证明;
(3)设函数h(x)=g(x)![]() (x>0),若h(2t)+mh(t)+4>0对任意的正实数t恒成立,求实数m的取值范围.
(x>0),若h(2t)+mh(t)+4>0对任意的正实数t恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD是边长为4的正方形,△PAD是一个正三角形,若平面PAD⊥平面ABCD,则该四棱锥的外接球的表面积为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,点
为坐标原点,点![]() 在圆
在圆![]() :
:![]() 上.
上.
(1)求实数![]() 的值;
的值;
(2)求过圆心![]() 且与直线
且与直线![]() 平行的直线的方程;
平行的直线的方程;
(3)过点![]() 作互相垂直的直线
作互相垂直的直线![]() ,
,![]() ,
,![]() 与圆
与圆![]() 交于
交于![]() 两点,
两点,![]() 与圆
与圆![]() 交于
交于![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 恰好在线段
恰好在线段![]() 的垂直平分线上,以
的垂直平分线上,以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且平面
的位置,且平面![]() 底面
底面![]() ,如图2所示,
,如图2所示,![]() 是线段
是线段![]() 的中点.
的中点.
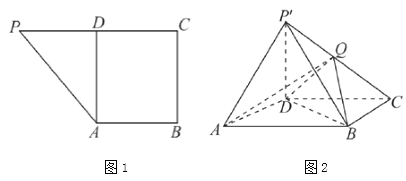
(1)证明:![]() 平面
平面![]() ;
;
(2)若三棱锥![]() 的体积为1,求
的体积为1,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为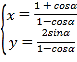 (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),将曲线
),将曲线![]() 向左平移2个单位长度得到曲线
向左平移2个单位长度得到曲线![]() .
.
(1)求曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,新能源汽车技术不断推陈出新,新产品不断涌现,在汽车市场上影响力不断增大.动力蓄电池技术作为新能源汽车的核心技术,它的不断成熟也是推动新能源汽车发展的主要动力.假定现在市售的某款新能源汽车上,车载动力蓄电池充放电循环次数达到2000次的概率为85%,充放电循环次数达到2500次的概率为35%.若某用户的自用新能源汽车已经经过了2000次充电,那么他的车能够充电2500次的概率为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com