
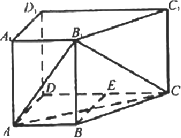
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0).
(1)求证:CD⊥平面ADD1A1;
(2)若直线AA1与平面AB1C所成角的正弦值为![]() ,求k的值;
,求k的值;
(3)现将与四棱柱ABCD-A1B1C1D1形状和大小完全相同的两个四棱柱拼接成一个新的棱柱,规定:若拼接成的新的四棱柱形状和大小完全相同,则视为同一种拼接方案.问:共有几种不同的方案?在这些拼接成的新四棱柱中,记其中最小的表面积为f(k),写出f(k)的表达式(直接写出答案,不必要说明理由)
|
本小题主要考查直线与直线.直线与平面的位置关系.柱体的概念及表面积等基础知识,考查空间想象能力.推理论证能力.运算求解能力,考查数形结合思想.分类与整合思想.化归与转化思想,满分13分. 解:(Ⅰ)取CD中点E,连接BE ∵AB∥DE ,AB=DE=3k 在△BCE中,∵BE=4k,CE=4k,BC=5k
(Ⅱ)以D为原点, 所以 设平面AB1C的法向量n=(x,y,z),则由 得 设AA1与平面AB1C所成角为 (Ⅲ)共有4种不同的方案 |


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2,四棱锥B-AA1C1D的体积为3.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2,四棱锥B-AA1C1D的体积为3.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.查看答案和解析>>
科目:高中数学 来源:四川省仁寿一中2012届高三12月月考数学理科试题 题型:044
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点F是棱C1D1的中点.

(1)若点E是棱CC1的中点,求证:EF∥平面A1BD;
(2)试确定点E的位置,使得A1-BD-E为直二面角,并说明理由.
查看答案和解析>>
科目:高中数学 来源:四川省仁寿一中2012届高三12月月考数学文科试题 题型:044
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点F是棱C1D1的中点.

(1)若点E是棱CC1的中点,求证:EF∥平面A1BD;
(2)试确定点E的位置,使得A1-BD-E为直二面角,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com