
分析 (1)求得二项式展开式的通项公式,化简整理,求出前三项的系数,得出一个关于n的方程,解出n;
(2)求出($\sqrt{x}$-$\frac{2}{x}$)9的通项,令x的指数为-3,求出r,继而求出x-3项的系数;
(3)令通项中x的指数为非负整数,求出符合条件的r,继而得出答案.
解答 解:(1)($\sqrt{x}$-$\frac{2}{x}$)n的展开式的通项公式为Tr+1=${C}_{n}^{r}$($\sqrt{x}$)n-r•(-$\frac{2}{x}$)r
=${C}_{n}^{r}$(-2)r•x${\;}^{\frac{n-3r}{2}}$,r=0,1,2,…,n,
由前3项的系数之和为127,
可得1+${C}_{n}^{1}$•(-2)+4${C}_{n}^{2}$=127,
化简得:n2-2n-63=0,
解得n=9或-7(舍),
所以n=9;
(2)由(1)可得Tr+1=${C}_{9}^{r}$(-2)r${x}^{\frac{9-3r}{2}}$,r=0,1,2,…,9,
令$\frac{9-3r}{2}$=-3,解得r=5,
可得x-3项的系数为${C}_{9}^{5}$(-2)5=-4032,
即为-4032;
(3)Tr+1=${C}_{9}^{r}$(-2)r${x}^{\frac{9-3r}{2}}$,r=0,1,2,…,9,
令$\frac{9-3r}{2}$为非负整数,
所以r可取1,3.
所以展开式中的所有整式项为:T2=-18x3,T4=-84.
点评 本题考查了二项式定理的应用:求特定项或系数,注意运用通项公式,考查了运算能力,属于中档题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:解答题
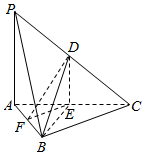 如图,在三棱锥P-ABC中,点D,E,F分别为棱PC,AC,AB的中点,已知PA⊥平面ABC,AB⊥BC,且AB=BC.
如图,在三棱锥P-ABC中,点D,E,F分别为棱PC,AC,AB的中点,已知PA⊥平面ABC,AB⊥BC,且AB=BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于直线y=0对称 | B. | 关于直线x=0对称 | C. | 关于直线y=a对称 | D. | 关于直线x=a对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{1}{5}$ | C. | $-\frac{{\sqrt{5}}}{5}$ | D. | $-\frac{1}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com