
分析 (1)由已知推导出a1=$\frac{3}{4}$,an=$\frac{1}{4}$an-1,由此能求出数列{an}的通项公式.
(2)先求出bn=(2n-7)cosnπ+3($\frac{1}{4}$)n,由此根据n为偶数和n为奇数两种情况分类讨论,能求出数列{bn}前n项和Tn.
解答 解:(1)∵数列{an}的前n项和为Sn,且Sn+$\frac{1}{3}$an=1(n∈N*),
∴当n=1时,a1=S1,由S1+$\frac{1}{3}$a1=$\frac{4}{3}{a}_{1}$=1,解得a1=$\frac{3}{4}$,
当n≥2时,Sn+$\frac{1}{3}$an=1,①,Sn-1+$\frac{1}{3}$an-1=1,②,
①-②,得an+$\frac{1}{3}$an-$\frac{1}{3}$an-1=0,即an=$\frac{1}{4}$an-1,
∴{an}是以$\frac{3}{4}$为首项,$\frac{1}{4}$为公比的等比数列.
∴an=$\frac{3}{4}$($\frac{1}{4}$)n-1=3($\frac{1}{4}$)n.(n∈N*).
(2)bn=[2log${\;}_{\frac{1}{4}}$($\frac{1}{3}$an)-7]cosnπ+an
=[$2lo{g}_{\frac{1}{4}}(\frac{1}{4})^{n}$-7]cosnπ+3($\frac{1}{4}$)n
=(2n-7)cosnπ+3($\frac{1}{4}$)n,
∴数列{bn}前n项和:
Tn=(7-2)+(4-7)+(7-8)+(16-7)+…+(2n-7)×(-1)n+3($\frac{1}{4}+\frac{1}{{4}^{2}}+\frac{1}{{4}^{3}}+\frac{1}{{4}^{4}}+…+\frac{1}{{4}^{n}}$),
∴当n为偶数时,
Tn=2+8+32+128+…+2×${4}^{\frac{n}{2}-1}$+3($\frac{1}{4}+\frac{1}{{4}^{2}}+\frac{1}{{4}^{3}}+\frac{1}{{4}^{4}}+…+\frac{1}{{4}^{n}}$)
=$\frac{2(1-{4}^{\frac{n}{2}})}{1-4}$+3×$\frac{\frac{1}{4}(1-\frac{1}{{4}^{n}})}{1-\frac{1}{4}}$
=$\frac{{2}^{n+1}}{3}$+$\frac{1}{3}$-$\frac{1}{{4}^{n}}$.
当n为奇数时,
Tn=2+8+32+128+…+2×${4}^{\frac{n-1}{2}}$+7-2n+3($\frac{1}{4}+\frac{1}{{4}^{2}}+\frac{1}{{4}^{3}}+\frac{1}{{4}^{4}}+…+\frac{1}{{4}^{n}}$)
=$\frac{2(1-{4}^{\frac{n-1}{2}})}{1-4}$+3×$\frac{\frac{1}{4}(1-\frac{1}{{4}^{n}})}{1-\frac{1}{4}}$+7-2n
=$\frac{{2}^{n}}{3}-\frac{1}{{4}^{n}}-2n+\frac{22}{3}$.
∴${b}_{n}=\left\{\begin{array}{l}{\frac{{2}^{n+1}}{3}+\frac{1}{3}-\frac{1}{{4}^{n}},n为偶数}\\{\frac{{2}^{n}}{3}-\frac{1}{{4}^{n}}-2n+\frac{22}{3}.n为奇数}\end{array}\right.$.
点评 本题考查数列的通项公式的求法,考查数列的前n项和的求法,是中档题,解题时要认真审题,注意构造法和分类讨论思想的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
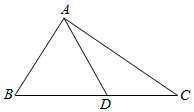 如图,D是直角三角形△ABC斜边BC上一点,AC=$\sqrt{3}$DC.
如图,D是直角三角形△ABC斜边BC上一点,AC=$\sqrt{3}$DC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com