
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
分析 (1)散点图如图:由图可判断:广告费与销售额具有相关关系.
(2)先求出$\overline{x}$、$\overline{y}$的值,可得 $\sum_{i=1}^5{{x_i}{y_i}}$ 和$\sum_{i=1}^5{x_i^2}$ 的值,从而求得 $b=\frac{{\sum_{i=1}^5{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^5{x_i^2-n\overline{x^2}}}}$和,$a=\overline y-b\overline x$的值,从而求得线性回归方程.
(3)在回归方程中,令y=115,求得x的值,可得结论.
解答 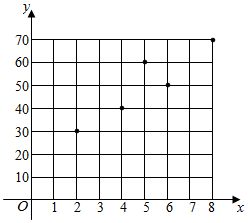 解:(1)散点图如图:由图可判断:广告费与销售额具有相关关系.
解:(1)散点图如图:由图可判断:广告费与销售额具有相关关系.
(2)∵$\overline x=\frac{1}{5}(2+4+5+6+8)=5$,$\overline y=\frac{1}{5}(30+40+60+50+70)=50$,
∴$\sum_{i=1}^5{{x_i}{y_i}}$=2×30+4×40+5×60+6×50+8×70=1380,$\sum_{i=1}^5{x_i^2}$=22+42+52+62+82=145,
∴$b=\frac{{\sum_{i=1}^5{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^5{x_i^2-n\overline{x^2}}}}$=$\frac{1380-5×5×50}{{145-5×{5^2}}}$=6.5,$a=\overline y-b\overline x$=50-6.5×5=17.5,
∴线性回归方程为 y=6.5x+17.5.
(3)令y=115,可得6.5×x+17.5=115,求得x=15,故预测销售额为115万元时,
大约需要15万元广告费.
点评 本题主要考查线性回归问题,求回归直线的方程,以及回归方程的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{9}{4}$ | D. | $\frac{16}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于直线y=0对称 | B. | 关于直线x=0对称 | C. | 关于直线y=a对称 | D. | 关于直线x=a对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com