Question

20．已知不等式组$\left\{\begin{array}{l}3x+4y-10≥0\\ x≤4\\ y≤3\end{array}\right.$，表示区域D，过区域D中任意一点P作圆x²+y²=1的两条切线且切点分别为A，B，当∠PAB最大时，cos∠PAB=（　　）

• A． $\frac{4}{5}$
• B． $\frac{1}{2}$
• C． $\frac{1}{5}$
• D． $\frac{3}{5}$

Answer 1

分析 由题意和线性规划问题画出平面区域D，由分析和切线性质得：要使∠PAB最大则∠OPA最小、即OP最大，由图象求出OP的最大值，根据诱导公式求出当∠PAB最大时cos∠PAB的值．

解答 解：由题意画出平面区域D如图所示，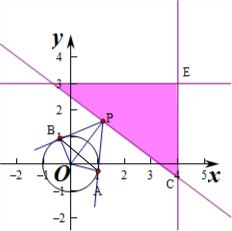
要使∠PAB最大，则∠OPA最小，
∵OA⊥PA，且OA=1，∴sin∠OPA=$\frac{OA}{OP}$=$\frac{1}{OP}$，
∴∠OPA最小，则sin∠OPA=$\frac{1}{OP}$最小，即OP最大，
∵点P是区域D中任意一点，
∴OP最大值是OE=$\sqrt{{4}^{2}+{3}^{2}}$=5，
此时sin∠OPA=$\frac{1}{5}$，
在RT△AOP中，∠PAB+∠OPA=$\frac{π}{2}$，
∴cos∠OPA=sin∠OPA=$\frac{1}{5}$，
故选：C．

点评 本题考查了直线与圆相切问题，线性规划的应用，利用数形结合是解决本题的关键，是综合性题目．