
分析 先化简p,q,根据¬q的一个充分不必要条件是¬p等价于p是q的一个必要不充分条件,分类讨论即可求出a的取值范围.
解答 解:由$\frac{4}{x-1}$≤-1,得p:-3≤x<1,----------------------------------------------(2分)
由x2+x<a2-a得(x+a)[x-(a-1)]<0,------------------------(3分)
当a=$\frac{1}{2}$时,q:∅;
当a<$\frac{1}{2}$时,q:(a-1,-a);
当a>$\frac{1}{2}$时,q:(-a,a-1).----------------------------------------------------------(6分)
由题意得,p是q的一个必要不充分条件,
当a=$\frac{1}{2}$时,满足条件;
当a<$\frac{1}{2}$时,(a-1,-a)⊆[-3,1]得a∈[-1,$\frac{1}{2}$),
当a>$\frac{1}{2}$时,(-a,a-1)⊆[-3,1]得a∈($\frac{1}{2}$,2],--------------------------------(10分)
综上,a∈[-1,2]---------------------------------------------------------------------------(12分)
点评 本题考查了充分必要条件,考查了集合之间的关系,是一道中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
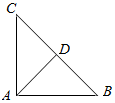 如图△ABC是直角边等于4的等腰直角三角形,D是斜边BC的中点,$\overrightarrow{AM}$=$\frac{1}{4}\overrightarrow{AB}$+m•$\overrightarrow{AC}$,向量$\overrightarrow{AM}$的终点M在△ACD的内部(不含边界),则实数m的取值范围是($\frac{1}{4}$,$\frac{3}{4}$).
如图△ABC是直角边等于4的等腰直角三角形,D是斜边BC的中点,$\overrightarrow{AM}$=$\frac{1}{4}\overrightarrow{AB}$+m•$\overrightarrow{AC}$,向量$\overrightarrow{AM}$的终点M在△ACD的内部(不含边界),则实数m的取值范围是($\frac{1}{4}$,$\frac{3}{4}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-y=0 | B. | x+y=0 | C. | x-y-2=0 | D. | x+y-2=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图“月亮图”是由曲线C1与C2构成,曲线C1是以原点O为中心,F1(-1,0),F2(1,0)为焦点的椭圆的一部分,曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A($\frac{3}{2}$,$\sqrt{6}$)是两条曲线的一个交点.
如图“月亮图”是由曲线C1与C2构成,曲线C1是以原点O为中心,F1(-1,0),F2(1,0)为焦点的椭圆的一部分,曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A($\frac{3}{2}$,$\sqrt{6}$)是两条曲线的一个交点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com