
 如图“月亮图”是由曲线C1与C2构成,曲线C1是以原点O为中心,F1(-1,0),F2(1,0)为焦点的椭圆的一部分,曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A($\frac{3}{2}$,$\sqrt{6}$)是两条曲线的一个交点.
如图“月亮图”是由曲线C1与C2构成,曲线C1是以原点O为中心,F1(-1,0),F2(1,0)为焦点的椭圆的一部分,曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A($\frac{3}{2}$,$\sqrt{6}$)是两条曲线的一个交点.分析 (Ⅰ)设曲线C2所在的抛物线的方程为y2=2px,将A($\frac{3}{2}$,$\sqrt{6}$)代入可得p的值,利用椭圆的定义,可得曲线C1所在的椭圆的方程;
(Ⅱ)设B(x1,y1),E(x2,y2),C(x3,y3),D(x4,y4),过F2与x轴不垂直的直线为x=ty+1,与椭圆方程联立,利用韦达定理可得|y1-y2|=$\frac{\sqrt{(16t)^{2}-4•(-64)•(9+8{t}^{2})}}{9+8{t}^{2}}$,同理可得|y3-y4|=$\sqrt{16{t}^{2}+16}$,进而可得$\frac{|BE|•|G{F}_{2}|}{|CD|•|H{F}_{2}|}$为定值.
解答 解:(Ⅰ)设曲线C2所在的抛物线的方程为y2=2px,将A($\frac{3}{2}$,$\sqrt{6}$)代入可得6=2p×$\frac{3}{2}$,∴p=2
∴曲线C2所在的抛物线方程为:y2=4x…(2分)
∴c=1,2a=$\sqrt{(\frac{3}{2}+1)^{2}+(\sqrt{6})^{2}}$+$\sqrt{(\frac{3}{2}-1)^{2}+(\sqrt{6})^{2}}$=6,
∴曲线C1所在的椭圆的方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{8}$=1. …(4分)
(Ⅱ)设B(x1,y1),E(x2,y2),C(x3,y3),D(x4,y4),过F2与x轴不垂直的直线为x=ty+1,与椭圆方程联立,消去x可得(9+8t2)y2+16ty-64=0,
∴y1+y2=-$\frac{16t}{9+8{t}^{2}}$,y1y2=-$\frac{64}{9+8{t}^{2}}$-,…(6分)
∴|y1-y2|=$\frac{\sqrt{(16t)^{2}-4•(-64)•(9+8{t}^{2})}}{9+8{t}^{2}}$
直线x=ty+1,与抛物线方程联立,消去x可得y2-4ty-4=0,∴y3+y4=4t,y3y4=-4…(8分)
∴|y3-y4|=$\sqrt{16{t}^{2}+16}$
∴$\frac{|BE|•|G{F}_{2}|}{|CD|•|H{F}_{2}|}$=$\frac{|{y}_{1}-{y}_{2}|•\frac{1}{2}|{y}_{3}+{y}_{4}|}{|{y}_{3}-{y}_{4}|•\frac{1}{2}|{y}_{1}+{y}_{2}|}$=$\frac{\frac{\sqrt{(16t)^{2}-4(-64)(9+8{t}^{2})}}{9+8{t}^{2}}•|4t|}{\sqrt{16{t}^{2}+16•\frac{|16t|}{9+8{t}^{2}}}}$=3
即$\frac{|BE|•|G{F}_{2}|}{|CD|•|H{F}_{2}|}$为定值3 …(13分)
点评 本题考查椭圆、抛物线的标准方程,考查直线与椭圆、抛物线的位置关系,考查韦达定理的运用,考查学生的计算能力,联立方程,正确运用韦达定理是关键.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | $\sqrt{2}$ | D. | $-\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
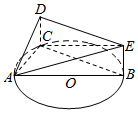 如图,AB是圆O的直径,点C在圆O上,矩形DCBE所在的平面垂直于圆O所在的平面,AB=4,BE=1.
如图,AB是圆O的直径,点C在圆O上,矩形DCBE所在的平面垂直于圆O所在的平面,AB=4,BE=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>a>b | B. | c>b>a | C. | a>c>b | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $4\sqrt{2}$ | C. | $4\sqrt{3}$ | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com