


科目:高中数学 来源: 题型:
| 1 |
| 8 |
| 1 |
| 8 |
| A、a>b>c |
| B、c>b>a |
| C、c>a>b |
| D、a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:
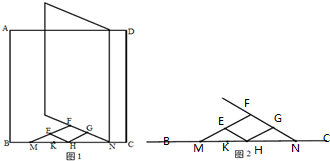 如图1是某窗户的窗扣示意图,图2是其俯视图,其中点E、F、G、M、K是固定点,点H是窗沿糟内可滑动点,点N是窗户下边沿延长线与窗沿的交点,窗户打开时,点H、N向点K移动,当点H移至点K时,不能再往左移动,此时窗户最大打开,窗户关闭时,点H、N向点C移动,当点N移动至点C时,点E、F、G落在BC上窗户刚好全部关闭.在窗户打开与关闭的过程中,四边形EFGH始终保持平行四边形的形状,现测得BM=18cm,MK=12cm,ME=EF,FG=GN,且HE=6cm,HG=10cm;
如图1是某窗户的窗扣示意图,图2是其俯视图,其中点E、F、G、M、K是固定点,点H是窗沿糟内可滑动点,点N是窗户下边沿延长线与窗沿的交点,窗户打开时,点H、N向点K移动,当点H移至点K时,不能再往左移动,此时窗户最大打开,窗户关闭时,点H、N向点C移动,当点N移动至点C时,点E、F、G落在BC上窗户刚好全部关闭.在窗户打开与关闭的过程中,四边形EFGH始终保持平行四边形的形状,现测得BM=18cm,MK=12cm,ME=EF,FG=GN,且HE=6cm,HG=10cm;查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| 1 |
| x |
| A、0个 | B、1个 | C、2个 | D、3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com