
分析 (1)求出函数的导数,解关于导函数的不等式求出函数的最小值即可;(2)解方程组,求出a的表达式,根据函数的单调性证明即可.
解答 解:(1)函数f(x)的定义域为(0,+∞),
求导得:${f^/}(x)=\frac{2}{x}-2x=\frac{2(1-x)(1+x)}{x}$,
则当$x∈[\frac{1}{e},1]$时,f′(x)>0,当x∈[1,e]时,f′(x)<0,
即f(x)在$[\frac{1}{e},1]$上单调递增,在[1,e]单调递减,
又$f(\frac{1}{e})=-2-\frac{1}{e^2},f(e)=2-{e^2},f(1)=-1$,且$f(\frac{1}{e})>f(e)$
因此,当x=1时,f(x)取得最大值-1,
当x=e时,f(x)取得最小值2-e2;
证明:(2)方程f(x)-ax=0有两个不等实根x1,x2,
则有$\left\{\begin{array}{l}2ln{x_1}-x_1^2-a{x_1}=0\\ 2ln{x_2}-x_2^2-a{x_2}=0\end{array}\right.$,
两式相减得,$a=\frac{{2(ln{x_1}-ln{x_2})}}{{{x_1}-{x_2}}}-({x_1}+{x_2})$,
又由已知$g{\;}^/(x)=\frac{2}{x}-2x-a$,
则${g^/}(\frac{{{x_1}+{x_2}}}{2})=\frac{4}{{{x_1}+{x_2}}}-({x_1}+{x_2})-a=\frac{4}{{{x_1}+{x_2}}}-({x_1}+{x_2})-[\frac{{2(ln{x_1}-ln{x_2})}}{{{x_1}-{x_2}}}-({x_1}+{x_2})]$,
即${g^/}(\frac{{{x_1}+{x_2}}}{2})=\frac{4}{{{x_1}+{x_2}}}-\frac{{2(ln{x_1}-ln{x_2})}}{{{x_1}-{x_2}}}$;
因此,${g^/}(\frac{{{x_1}+{x_2}}}{2})<0$$?\frac{4}{{{x_1}+{x_2}}}-\frac{{2(ln{x_1}-ln{x_2})}}{{{x_1}-{x_2}}}<0?\frac{{2({x_1}-{x_2})}}{{{x_1}+{x_2}}}>ln{x_1}-ln{x_2}(∵0<{x_1}<{x_2})$$?\frac{{2(\frac{x_1}{x_2}-1)}}{{\frac{x_1}{x_2}+1}}>ln\frac{x_1}{x_2}$,
令$h(t)=\frac{2(t-1)}{t+1}-lnt,t∈(0,1)$,则${h^/}(t)=\frac{4}{{{{(t+1)}^2}}}-\frac{1}{t}=-\frac{{{{(t-1)}^2}}}{{t{{(t+1)}^2}}}<0$,即函数h(t)在(0,1)上递减,
所以,当t∈(0,1)时,h(t)>h(1)=0,即$\frac{2(t-1)}{t+1}>lnt(0<t<1)$,
因此,当0<x1<x2时,$\frac{{2(\frac{x_1}{x_2}-1)}}{{\frac{x_1}{x_2}+1}}>ln\frac{x_1}{x_2}$成立,即${g^/}(\frac{{{x_1}+{x_2}}}{2})<0$成立.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的证明,是一道中档题.


 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,x,1,2} | B. | {1,2,0,1} | C. | {0,1,2} | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
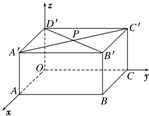 如图,长方体OABC-D′A′B′C′中,|OA|=3,|OC|=4,|OD′|=5,B′D′与A′C′交于P,则点P的坐标为($\frac{3}{2}$,2,5).
如图,长方体OABC-D′A′B′C′中,|OA|=3,|OC|=4,|OD′|=5,B′D′与A′C′交于P,则点P的坐标为($\frac{3}{2}$,2,5).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 正三棱柱被一个平面截去一部分后与半圆柱组成一个几何体,该几何体的三视图如图所示,则该几何体的体积为( )
正三棱柱被一个平面截去一部分后与半圆柱组成一个几何体,该几何体的三视图如图所示,则该几何体的体积为( )| A. | $2π+\sqrt{3}$ | B. | $π+\sqrt{3}$ | C. | $π+\frac{{4\sqrt{3}}}{3}$ | D. | $π+\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com