
分析 (1)使用二倍角公式化简f(x),根据f($\frac{π}{3}$)=3,f($\frac{5π}{6}$)=1列方程组解出a,b;
(2)根据x的范围得出x+$\frac{π}{6}$的范围,利用正弦函数的单调性求出f(x)的值域.
解答 解:(1)f(x)=acosx+$\sqrt{3}$asinx+b=2asin(x+$\frac{π}{6}$)+b.
∵f($\frac{π}{3}$)=3,f($\frac{5π}{6}$)=1,
∴$\left\{\begin{array}{l}{2a+b=3}\\{b=1}\end{array}\right.$,解得a=1,b=1.
(2)由(1)得:$f(x)=2sin(x+\frac{π}{6})+1$,
∵x∈[0,$\frac{π}{2}$],∴x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{2π}{3}$].
∴当x+$\frac{π}{6}$=$\frac{π}{6}$时,f(x)取得最小值2×$\frac{1}{2}+1$=2,
当x+$\frac{π}{6}$=$\frac{π}{2}$时,f(x)取得最大值2×1+1=3.
∴f(x)在[0,$\frac{π}{2}}$]上的值域为[2,3].
点评 本题考查了三角函数的恒等变换,正弦函数的性质,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,某汽车前灯的反光曲面与轴截面的交线为抛物线的一部分,灯口直径AB为140$\sqrt{2}$mm,反光曲面的顶点O到灯口的距离是70mm,由抛物线的性质可知,当灯泡安装在抛物线的焦点处时,经反光曲面反射的光束是平行光束,问:为了获得平行光束,应怎样安装灯泡?
如图,某汽车前灯的反光曲面与轴截面的交线为抛物线的一部分,灯口直径AB为140$\sqrt{2}$mm,反光曲面的顶点O到灯口的距离是70mm,由抛物线的性质可知,当灯泡安装在抛物线的焦点处时,经反光曲面反射的光束是平行光束,问:为了获得平行光束,应怎样安装灯泡?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,已知抛物线C:y2=2px(p>0)的焦点是F,抛物线C上的横坐标为1的点到焦点F的距离是2,直线l经过点F交抛物线C于A、B两点,A点在x轴下方,点D和点A关于x轴对称.
如图所示,已知抛物线C:y2=2px(p>0)的焦点是F,抛物线C上的横坐标为1的点到焦点F的距离是2,直线l经过点F交抛物线C于A、B两点,A点在x轴下方,点D和点A关于x轴对称.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
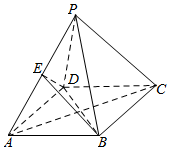 如图,正四棱锥P-ABCD中,底面ABCD的边长为4,PD=4,E为PA的中点,
如图,正四棱锥P-ABCD中,底面ABCD的边长为4,PD=4,E为PA的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com