
【题目】设动点![]() 到定点
到定点![]() 的距离比它到
的距离比它到![]() 轴的距离大
轴的距离大![]() ,记点
,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)若圆心在曲线![]() 上的动圆
上的动圆![]() 过点
过点![]() ,试证明圆
,试证明圆![]() 与
与![]() 轴必相交,且截
轴必相交,且截![]() 轴所得的弦长为定值.
轴所得的弦长为定值.
【答案】(1) ![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)根据抛物线定义判断点![]() 的轨迹,再根据抛物线几何条件求标准方程,(2)结合题意设出圆心
的轨迹,再根据抛物线几何条件求标准方程,(2)结合题意设出圆心![]() 的坐标,并根据圆过点A得到圆的标准方程,在圆方程中令
的坐标,并根据圆过点A得到圆的标准方程,在圆方程中令![]() 后可得关于x的二次方程,根据此方程判别式可判断圆与x轴相交,同时并根据数轴上两点间的距离求出弦长.
后可得关于x的二次方程,根据此方程判别式可判断圆与x轴相交,同时并根据数轴上两点间的距离求出弦长.
试题解析:(1)依题意知,动点![]() 到定点
到定点![]()
![]() 的距离等于
的距离等于![]() 到直线
到直线![]() 的距离,
的距离,
∴曲线![]() 是以原点为顶点,
是以原点为顶点, ![]()
![]() 为焦点的抛物线.
为焦点的抛物线.
设曲线C的方程为![]() ,
,
则![]() , ∴
, ∴![]() ,∴曲线
,∴曲线![]() 方程是
方程是![]() .
.
(2)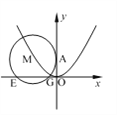
设圆心为![]() ,则
,则![]() ,
,
∵圆![]() 过
过![]()
![]() ,∴圆的方程为
,∴圆的方程为![]() ,
,
令![]() 得
得![]() .
.
∵![]() ∴圆
∴圆![]() 与
与![]() 轴必相交,
轴必相交,
设圆M与![]() 轴的两交点分别为E
轴的两交点分别为E ![]() ,G
,G![]()
则![]() ,
, ![]() ,
,
∴![]()
![]()
![]() ,
,
∴![]() =4.
=4.
故圆截![]() 轴所得的弦长为定值.
轴所得的弦长为定值.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:
【题目】若存在一个实数![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的一个不动点,设函数
的一个不动点,设函数![]() (
(![]() ,
, ![]() 为自然对数的底数),定义在
为自然对数的底数),定义在![]() 上的连续函数
上的连续函数![]() 满足
满足![]() ,且当
,且当![]() 时,
时, ![]() .若存在
.若存在![]() ,且
,且![]() 为函数
为函数![]() 的一个不动点,则实数
的一个不动点,则实数![]() 的取值范围为( )
的取值范围为( )
A. 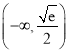 B.
B.  C.
C. 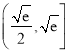 D.
D. 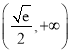
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+1+|3-x|,x≥-1.
(1)求不等式f(x)≤6的解集;
(2)若f(x)的最小值为n,正数a,b满足2nab=a+2b,求2a+b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某市11月1日至14日的空气质量指数趋势图,空气质量指数(AQI)小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择11月1日至11月12日中的某一天到达该市,并停留3天.
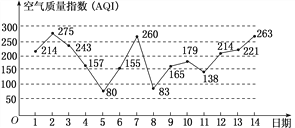
(1)求此人到达当日空气重度污染的概率;
(2)设X是此人停留期间空气重度污染的天数,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中有如下间题:“今有甲、乙、丙、丁、戊五人分五饯,令上二人所得与下三人等,且五人所得钱按顺序等次差,问各得几何?”其意思为“甲、乙、丙、丁、戊五人分五钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列,问五人各得多少钱(钱:古代一种重量单位)?”这个问题中丙所得为( )
A. ![]() 钱 B.
钱 B. ![]() 钱 C. 1钱 D.
钱 C. 1钱 D. ![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的公差
的公差![]() 大于0,且
大于0,且![]() ,
,![]() 是方程
是方程![]() 的两根,数列
的两根,数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,试比较
,试比较![]() 与
与![]() 的大小,并用数学归纳法给予证明.
的大小,并用数学归纳法给予证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.

(1)如图,设直线![]() 将坐标平面分成
将坐标平面分成![]() 四个区域(不含边界),若函数
四个区域(不含边界),若函数![]() 的图象恰好位于其中一个区域内,判断其所在的区域并求对应的
的图象恰好位于其中一个区域内,判断其所在的区域并求对应的![]() 的取值范围;
的取值范围;
(2)当![]() 时,求证:
时,求证:![]() 且
且![]() ,有
,有![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com