
【题目】如图所示,在几何体![]() 中,四边形
中,四边形![]() 是菱形,
是菱形,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 是直二面角,求异面直线
是直二面角,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.

【答案】(1)见解析;(2)![]()
【解析】
(1)通过证明![]() ,
,![]() ,证明
,证明![]() 平面
平面![]() ,再得到平面
,再得到平面![]() ⊥平面
⊥平面![]() .
.
(2)以![]() 为
为![]() 轴和
轴和![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,设
,设![]() ,求出平面
,求出平面![]() 的法向量
的法向量![]() 和平面
和平面![]() 的法向量
的法向量![]() ,利用二面角
,利用二面角![]() 是直二面角求出
是直二面角求出![]() ,得到
,得到![]() 与
与![]() 的坐标,利用向量夹角公式,得到答案.
的坐标,利用向量夹角公式,得到答案.
(1)证明:![]() 四边形
四边形![]() 是菱形,
是菱形,![]()
![]() 平面
平面![]() ,
,![]()
而![]()
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ⊥平面
⊥平面![]()
(2)设![]() 与
与![]() 的交点为
的交点为![]() ,由(1)得
,由(1)得![]() ,
,
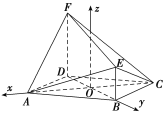
如图:分别以![]() 为
为![]() 轴和
轴和![]() 轴,过点
轴,过点![]() 作垂直于平面
作垂直于平面![]() 的直线为
的直线为![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]()
![]() .设
.设![]() ,
,
则![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则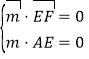 ,
,
即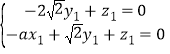 ,
,
令![]() ,
,![]() 平面AEF的一个法向量为
平面AEF的一个法向量为![]()
同理设![]() ,是平面
,是平面![]() 的法向量,则
的法向量,则
得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
![]() 二面角
二面角![]() 是直二面角,
是直二面角,
![]() ,
,![]() .
.
![]() ,
,![]()
设异面直线![]() 与
与![]() 所成角为
所成角为![]()

![]()
故所求异面直线![]() 与
与![]() 所成角为的余弦值为
所成角为的余弦值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求![]() 的最小正周期;
的最小正周期;
(2)求![]() 的值域;
的值域;
(3)求![]() 的递增区间
的递增区间
(4)求![]() 的对称轴;
的对称轴;
(5)求![]() 的对称中心;
的对称中心;
(6)![]() 的三边a,b,c满足
的三边a,b,c满足![]() ,且b所对的角为x,求x的取值范围及函数
,且b所对的角为x,求x的取值范围及函数![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ,σ2).
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在(μ-3σ,μ+3σ)之外的零件数,求P(X≥1)及X的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在(μ-3σ,μ+3σ)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
①试说明上述监控生产过程方法的合理性;
②下面是检验员在一天内抽取的16个零件的尺寸:

经计算得![]() =
=![]() =9.97,s=
=9.97,s=![]() =
=![]() ≈0.212,其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
≈0.212,其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
用样本平均数![]() 作为μ的估计值
作为μ的估计值![]() ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值![]() ,,利用估计值判断是否需对当天的生产过程进行检查?剔除(
,,利用估计值判断是否需对当天的生产过程进行检查?剔除(![]() ﹣3
﹣3![]() +3
+3![]() )之外的数据,用剩下的数据估计μ和σ(精确到0.01).
)之外的数据,用剩下的数据估计μ和σ(精确到0.01).
附:若随机变量Z服从正态分布N(μ,σ2),则P(μ-3σ<Z<μ+3σ)=0.997 4.0.997 416≈0.959 2,![]() ≈0.09.
≈0.09.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设动点![]() 到定点
到定点![]() 的距离比它到
的距离比它到![]() 轴的距离大
轴的距离大![]() ,记点
,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)若圆心在曲线![]() 上的动圆
上的动圆![]() 过点
过点![]() ,试证明圆
,试证明圆![]() 与
与![]() 轴必相交,且截
轴必相交,且截![]() 轴所得的弦长为定值.
轴所得的弦长为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程
的参数方程![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为: ![]() .
.
(1)把直线![]() 的参数方程化为极坐标方程,把曲线
的参数方程化为极坐标方程,把曲线![]() 的极坐标方程化为普通方程;
的极坐标方程化为普通方程;
(2)求直线![]() 与曲线
与曲线![]() 交点的极坐标(
交点的极坐标(![]() ≥0,0≤
≥0,0≤![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着“一带一路”倡议的推进,中国与沿线国家旅游合作越来越密切,中国到“一带一路”沿线国家的游客人也越来越多,如图是2013-2018年中国到“一带一路”沿线国家的游客人次情况,则下列说法正确的是( )
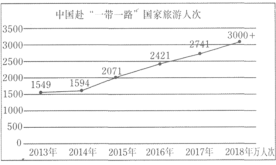
①2013-2018年中国到“一带一路”沿线国家的游客人次逐年增加
②2013-2018年这6年中,2016年中国到“一带一路”沿线国家的游客人次增幅最小
③2016-2018年这3年中,中国到“一带一路”沿线国家的游客人次每年的增幅基本持平
A.①③B.②③C.①②D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() :
:![]()
![]() 的离心率为
的离心率为![]() ,抛物线
,抛物线![]() :
:![]() 截
截![]() 轴所得的线段长等于
轴所得的线段长等于![]() .
.![]() 与
与![]() 轴的交点为
轴的交点为![]() ,过点
,过点![]() 作直线
作直线![]() 与
与![]() 相交于点
相交于点![]() 直线
直线![]() 分别与
分别与![]() 相交于
相交于![]() .
.
(1)求证:![]() ;
;
(2)设![]() ,
,![]() 的面积分别为
的面积分别为![]() ,若
,若![]()
![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com